 |
Элементы теории вероятности и математической статистики
|
|
|
|
Кафедра общей химии
 |
Часть I
ФИЗИЧЕСКАЯ ХИМИЯ
Учебно-методическое пособие
для аудиторной и внеаудиторной работы
студентов фармацевтического факультета
Рекомендовано Учебно-методическим объединением по медицинскому и фармацевтическому образованию вузов России в качестве учебного пособия для студентов, обучающихся по специальности 060108 (040500) – Фармация
Краснодар
УДК 541.1
ББК 24.5
Ш 42
Составители:
доктор хим. наук, профессор Н.В. Шельдешов,
канд. пед. наук, ассистент О.В. Балачевская,
канд. хим. наук, ассистент Д.А. Хосроева
Под редакцией зав. кафедрой общей химии КГМУ, профессора, д.п.н. Т.Н. Литвиновой
Рецензенты:
– зав. кафедрой общей и биоорганической химии Волгоградской государственной медицинской академии, профессор, д.х.н. А.К. Брель.
– зав. кафедрой биоорганической и биофизической химии
Ярославской медицинской академии, к.б.н. Т.Ю. Широкова.
Задачи по физической и коллоидной химии: часть I Физическая химия: Учебно-методическое пособие. – Краснодар, КГМУ, 2009 – 350 с.
Учебно-методическое пособие составлено на основе примерной программы по дисциплине физическая и коллоидная химия, утвержденной в 2002 г., и предназначено для студентов фармацевтического факультета.
Решение УМО МЗ и СР РФ
УМО – 790
16.11.07
СОДЕРЖАНИЕ
ВВЕДЕНИЕ............................................................................................... 5
ВВОДНЫЙ БЛОК ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ................................................. 5
1. Элементы теории вероятности и математической статистики 5
Примеры решения задач............................................................... 5
|
|
|
Задачи и упражнения для самостоятельного решения........... 5
2. Ошибки измерений......................................................................... 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
3. Округление чисел........................................................................... 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
4. Построение графиков..................................................................... 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
5. Расчет коэффициентов прямой..................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
6. Линеаризация................................................................................... 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
7. Нахождение производных и интегрирование............................ 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
1. ФИЗИЧЕСКАЯ ХИМИЯ.................................................................... 5
МОДУЛЬ 1 ТЕРМОДИНАМИКА. ТЕРМОХИМИЯ......................... 5
1.1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ ТЕРМОДИНАМИКИ. ТЕРМОХИМИЯ.................................................................................... 5
1.1.1. Первое начало термодинамики.............................................. 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.1.2. Термохимия............................................................................... 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.1.3. Второе начало термодинамики. Энтропия........................... 5
|
|
|
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.1.4. Термодинамические потенциалы. Функции Гиббса, Гельмгольца 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.2. ТЕРМОДИНАМИКА ХИМИЧЕСКОГО РАВНОВЕСИЯ...... 5
1.2.1. Изотерма химической реакции. Расчет констант равновесия химических реакций по термодинамическим таблицам..................................... 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.2.2. Зависимость констант равновесия реакций от температуры. Расчет равновесного выхода продуктов реакции...................................... 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
МОДУЛЬ 2 ХИМИЧЕСКОЕ РАВНОВЕСИЕ. ФАЗОВЫЕ РАВНОВЕСИЯ 5
1.3. ТЕРМОДИНАМИКА ФАЗОВЫХ РАВНОВЕСИЙ................. 5
1.3.1. Фазовые равновесия в однокомпонентных системах. Правило фаз Гиббса. Уравнения Клапейрона, Клапейрона – Клаузиуса........................ 5
Основные уравнения..................................................................... 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
1.3.2. Фазовые равновесия в двухкомпонентных системах, перегонка 5
Основные уравнения..................................................................... 5
1.3.3. Фазовые равновесия в трехкомпонентных системах. Экстракция 5
Примеры решения типовых задач.............................................. 5
Задачи для самостоятельного решения..................................... 5
МОДУЛЬ 3 КОЛЛИГАТИВНЫЕ СВОЙСТВА РАСТВОРОВ. ЭЛЕКТРОХИМИЯ...................................................................................................................... 5
1.4. ТЕРМОДИНАМИКА РАЗБАВЛЕННЫХ РАСТВОРОВ, ВЗАИМОСВЯЗЬ МЕЖДУ КОЛЛИГАТИВНЫМИ СВОЙСТВАМИ......................... 5
1.4.1. Давление пара растворителя над разбавленными растворами. Закон Рауля................................................................................................................ 5
|
|
|
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.4.2. Осмотическое давление растворов........................................ 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.4.3. Криоскопия. Эбуллиоскопия................................................. 5
Основные уравнения..................................................................... 5
Криоскопия................................................................................. 5
Эбулиоскопия............................................................................ 5
Экспериментальные методы определения молярных масс и изотонического коэффициента методом эбуллиоскопии и криоскопии 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.5. ТЕРМОДИНАМИКА РАСТВОРОВ ЭЛЕКТРОЛИТОВ........ 5
1.5.1. Теория растворов сильных электролитов Дебая – Хюккеля...... 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.5.2. Буферные системы и растворы............................................... 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.6. ЭЛЕКТРОХИМИЯ........................................................................ 5
1.6.1. Электропроводность растворов электролитов................... 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.6.2. Электродные потенциалы и электродвижущие силы гальванических элементов.............................................................................................. 5
1.6.2.1. Электроды и электродные потенциалы....................... 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
|
|
|
Задачи для самостоятельного решения..................................... 5
1.6.2.2. Гальванические элементы и ЭДС.................................. 5
Основные уравнения..................................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
МОДУЛЬ 4 КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ И КАТАЛИЗ 5
1.7. КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ................................ 5
1.7.1. Скорость реакции..................................................................... 5
Основные уравнения..................................................................... 5
Скорость реакции...................................................................... 5
Расчет скорости реакции по экспериментальным данным, заданным в виде таблицы....................................................................................... 5
Расчет скорости реакции по экспериментальным данным, заданным в виде графика........................................................................................ 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.7.2. Формальная кинетика необратимых реакций нулевого, первого, второго порядков............................................................................................... 5
Основные уравнения..................................................................... 5
Основной постулат химической кинетики – закон действия масс для кинетики...................................................................................... 5
Молекулярность химической реакции.................................. 5
Реакция нулевого порядка....................................................... 5
Реакция первого порядка......................................................... 5
Реакция второго порядка......................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.7.3. Методы определения порядков и констант скоростей реакций 5
Основные уравнения..................................................................... 5
Интегральные методы............................................................... 5
Метод подстановки.................................................. 5
Графический метод.................................................. 5
Определение порядка реакции по периоду полупревращения 5
Дифференциальные методы.................................................... 5
Метод Вант-Гоффа................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.7.4. Зависимость скорости реакции от температуры................. 5
Основные уравнения..................................................................... 5
Правило Вант-Гоффа................................................................ 5
Уравнение Аррениуса............................................................... 5
Метод ускоренного определения срока годности лекарственных препаратов.................................................................................. 5
|
|
|
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.7.5. Сложные реакции..................................................................... 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
1.7.6. Ферментативный катализ........................................................ 5
Примеры решения задач............................................................... 5
Задачи и упражнения для самостоятельного решения........... 5
МОДУЛЬ 5 ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ И АДСОРБЦИЯ....... 5
1.8. ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ И АДСОРБЦИЯ.................. 5
1.8.1. Термодинамика поверхностного слоя.................................. 5
Основные уравнения..................................................................... 5
Поверхностная энергия Гиббса и поверхностное натяжение 5
Методы определения поверхностного натяжения на легкоподвижных границах фаз............................................................................... 5
Краевой угол смачивания........................................................ 5
Зависимость поверхностного натяжения от температуры. Связь поверхностной энергии Гиббса и поверхностной энтальпии 5
Энтальпия смачивания и коэффициент гидрофильности.. 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.8.2. Адсорбция на границе «жидкость – газ»............................. 5
Основные уравнения..................................................................... 5
Уравнение изотермы адсорбции Гиббса................................ 5
Изотерма поверхностного натяжения.................................... 5
Поверхностно-активные, поверхностно-инактивные вещества, их молекулярное строение............................................................ 5
Ориентация молекул в поверхностном слое........................ 5
Адсорбция на границе «жидкость – газ». Уравнение Ленгмюра 5
Определение площади, занимаемой молекулой поверхностно-активного вещества в насыщенном адсорбционном слое, и максимальной длины молекулы ПАВ........................................................................... 5
Уравнение Шишковского......................................................... 5
Правило Дюкло – Траубе......................................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
1.8.3. Адсорбция на границе «твердое тело – газ» и «твердое тело – жидкость»................................................................................................................ 5
Основные уравнения..................................................................... 5
Мономолекулярная адсорбция, уравнение изотермы адсорбции Лэнгмюра, Фрейндлиха................................................................................ 5
Полимолекулярная адсорбция................................................ 5
Капиллярная конденсация....................................................... 5
Адсорбция электролитов. Неспецифическая (эквивалентная) адсорбция ионов. Избирательная адсорбция ионов. Правило Панета – Фаянса 5
Ионный обмен. Иониты и их классификация. Обменная емкость. Применение ионитов в фармации........................................... 5
Примеры решения задач............................................................... 5
Задачи для самостоятельного решения..................................... 5
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ............................................................... 5
ПРИЛОЖЕНИЕ........................................................................................ 5
1. Основные единицы измерения физических величин.................. 5
2. Основные физические постоянные................................................ 5
3. Основные математические формулы дифференциального и интегрального исчисления.............................................................................................. 5
Таблица производных элементарных функций............................. 5
Основные правила дифференцирования......................................... 5
Основные правила интегрирования................................................. 5
4. Критические значения коэффициента Стьюдента t.................... 5
5. Критические значения критерия Фишера F для α = 0,05.......... 5
6. Стандартные энтальпии плавления и испарения при температуре фазового перехода.................................................................................................. 5
7. Константы Генри (Па) при 25°С..................................................... 5
8. Криоскопические и эбуллиоскопические константы................. 5
9. Термодинамические свойства простых веществ, ионов и соединений 5
Простые вещества и ионы.................................................................. 5
Неорганические соединения.............................................................. 5
Органические соединения.................................................................. 5
Углеводороды................................................................................ 5
Кислородсодержащие соединения............................................. 5
Галогенсодержащие соединения................................................ 5
Азотсодержащие соединения...................................................... 5
10. Теплота сгорания питательных веществ в живом организме и в калориметре.................................................................................................................. 5
11. Криоскопические и эбуллиоскопические константы............... 5
12. Удельная электрическая проводимость растворов KCl.......... 5
13. Предельные молярные подвижности ионов в водном растворе при 25°С 5
14. Молярная электропроводность разбавленных водных растворов электролитов при 25°С........................................................................ 5
15. Константы диссоциации слабых кислот при 25°С.................... 5
16. Константы диссоциации слабых оснований при 25°С............. 5
17. Стандартные электродные потенциалы при 25°С..................... 5
18. Основные физические постоянные.............................................. 5
19. Плотность ПАВ в жидком состоянии......................................... 5
20. Зависимость поверхностного натяжения воды от температуры 5
ЛИТЕРАТУРА.......................................................................................... 5
ВВЕДЕНИЕ
Специалист в области фармацевтической химии должен не только знать физико-химические законы, но и уметь применять их для решения конкретных задач. Расчетные задачи, содержащиеся в учебно-методическом пособии, позволяют глубже понять теоретический материал и получить практические навыки физико-химических расчетов.
Данное пособие содержит методы математической и статистической обработки результатов эксперимента, необходимые для изучения физической и коллоидной химии и других специальных дисциплин. Вводный блок нацелен на углубление навыков, приобретенных студентами в процессе изучения математики (операции дифференцирования, нахождения производных, интегрирования). Кроме этого, студенты повторяют основные методы графической обработки данных (построение графиков, определение коэффициентов уравнения прямой по экспериментальным данным), метод линеаризации, применяют электронные таблицы Excel для определения параметров линейных уравнений методом наименьших квадратов. Данные компоненты содержания вводного блока находят применение в учебно-исследовательских лабораторных работах, практических и семинарских занятиях по физической и коллоидной химии на фармацевтическом факультете.
В каждом разделе учебно-методического пособия содержится краткое теоретические введение, содержащее сведения, необходимые для решения задач, и основные расчетные формулы. В конце каждой темы приведены решения типовых задач и задачи для самостоятельного решения с ответами, что помогает студентам лучше понять теоретический материал.
В конце учебно-методического пособия находится список основной и дополнительной литературы, а также предметный указатель, который позволяет быстро найти необходимую информацию в тексте.
ВВОДНЫЙ БЛОК
ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Элементы теории вероятности и математической статистики
Теория вероятностей – это раздел математики, изучающий объективные закономерности случайных событий и случайных величин. На основе теории вероятностей построена математическая статистика, занимающаяся разработкой методов сбора, описания и обработки результатов эксперимента.
В основе статистики лежит представление, что каждая группа экспериментальных значений любого данного типа есть случайная выборка из бесконечного числа сходных значений, называемого генеральной совокупностью. Например, при анализе трех растворов с истинной общей концентрацией уксусной кислоты, равной 0,10000 М, могут быть получены значения 0,1001, 0,0998 и 0,1003 М. Выборка состоит из трех чисел; генеральная совокупность включает все числа, которые могли бы быть получены при выполнении этого анализа тем же методом бесконечное число раз.
Во многих случаях в физико-химических измерениях частота появления чисел при большом количестве измерений описывается нормальным законом распределения случайных величин Гаусса (рис. 1):
 ,
| (1) |
где dN/N – часть генеральной совокупности, включающая числа в интервале между x и x + dx, μ – среднее из всех чисел генеральной совокупности, σ – стандартное отклонение генеральной совокупности, exp (а) = ea.
Распределение Гаусса называется нормальным в силу того, что многие распределения, отражающие самые разнообразные явления случайного характера, протекающие в природе, подчиняются этому закону. Согласно статистической теории ошибок при условии выполнения нормального закона среднее арифметическое из результатов измерений является наиболее вероятным значением измеряемой величины и это значение тем ближе к истинному значению m, чем больше проведено измерений.
Рис. 1. Кривая плотности вероятности нормально распределенной случайной величины х
Кривая нормального распределения (рис. 1) имеет колоколообразный вид и симметрична относительно x = μ. Это означает, что положительные отклонения при измерении этой величины так же вероятны, как и ее отрицательные отклонения. Площадь под кривой нормального распределения равна 1, следовательно, любое значение x лежит между – ¥ и + ¥.
Чтобы получить результат, как можно более близкий к истинному значению определяемой величины, измерения выполняют многократно и из них находят среднее арифметическое значение 
от всех измерений х 1, х 2, …, хn:
 ,
| (2) |
где n – количество выполненных измерений (объем выборки).
Удобной количественной мерой рассеяния случайной величины является дисперсия. Дисперсия отдельного измерения определяется по формуле:
 .
| (3) |
Величина n – 1 в уравнении называется числом степеней свободы f.
Дисперсия среднего значения случайной величины рассчитывается по формуле:
 .
| (4) |
Дисперсию удобно использовать в тех случаях, когда возникает задача сравнения двух методов измерения, например, сопоставить точность приборов, оценить равносильность методов и тому подобное. Предпочтение отдается тому методу, который обеспечивает наименьшее рассеяние результатов исследования, то есть наименьшую дисперсию.
В физико-химических расчетах часто используют среднее квадратичное отклонение отдельного измерения от среднего:
 ,
| (5) |
и среднее квадратичное отклонение среднего от истинного значения измеряемой величины:
 ,
| (6) |
так как они имеют такую же размерность, как и измеряемая величина.
Среднее квадратичное отклонение отдельного измерения 
является аналогом стандартного отклонения σ генеральной совокупности и тем ближе к нему, чем больше проведено измерений, т.е. чем больше объем выборки.
Подставляя уравнение (3) в уравнение (5), получаем выражение для среднего квадратичного отклонения отдельного измерения:
 .
| (7) |
В этой формуле суммируются квадраты единичных отклонений. Единичные отклонения называются также абсолютной ошибкой отдельного измерения. Они рассчитываются как отклонение отдельного измерения от среднего арифметического.
Дисперсия входит в уравнение для расчета критерия Фишера, который используется для выяснения того, принадлежат ли две выборки случайной величины одной и той же генеральной совокупности:
 ,
| (8) |
где sN и sD – выборочные стандартные отклонения для двух выборок, причем 
. Рассчитанное по экспериментальным данным значение F сравнивают с критическим значением, которое находят по таблице значений критерия Фишера (Приложение 5). Если рассчитанное значение F меньше найденного в таблице, можно утверждать, что между обоими сравниваемыми значениями s различие не значимо.
Поскольку часто проводится не слишком много измерений нормально распределенной случайной величины, то параметры генеральной совокупности μ и σ, их аналогами для малой выборки являются и известны не точно.
В малых выборках случайная величина распределена не по закону нормального распределения, а по распределению Стьюдента (рис. 2), которое переходит в нормальное распределение при бесконечно большом числе измерений.
Доверительный интервал (доверительный интервал среднего) – это интервал, в котором с заданной доверительной вероятностью Р находится истинное значение определяемой величины μ:
,
где 
– полуширина доверительного интервала, которая определяется по формуле:
 ,
| (9) |
где t α – коэффициент Стьюдента, зависящий от доверительной вероятности Р и объема выборки n.
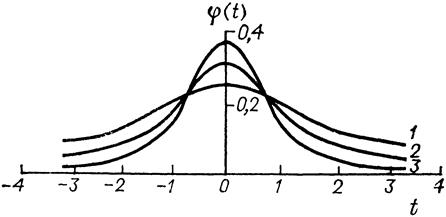
Рис. 2. Зависимость плотности вероятности φ (t) от ширины доверительного интервала t для распределения Стьюдента при разном числе степеней свободы f, равном 1, 2 и 3
Доверительная вероятностьР – вероятность нахождения истинного значения определяемой величины в пределах доверительного интервала:
 .
| (10) |
Например, доверительный интервал для вероятности 95% определяется неравенством:
 .
| (11) |
В этот интервал истинное значение определяемой величины μ попадает в 95% случаев. Смысл доверительного интервала из этого примера достаточно ясен: мы не знаем точно, чему равно истинное значение измеряемой величины, но можем указать с заданной вероятностью интервал, в котором оно находится.
Этот способ определения доверительного интервала с помощью критерия Стьюдента можно применять только в том случае, когда измеряемая величина распределена по нормальному закону.
Физико-химические измерения, как правило, подвержены воздействию случайных факторов и поэтому их результат имеет вероятностный характер. Следовательно, должна быть указана некоторая вероятность Р, которая соответствует уровню значимости α = 1 – Р, означающая, что ошибка измерения не превзойдет критическое значение. Основанием для выбора того или иного значения α чаще всего служат соображения практического характера, с учетом которых значение α обычно выбирают из интервала [0,001; 0,1].
Значения коэффициентов Стьюдента t для соответствующих доверительных вероятностей Р при различных числах степеней свободы f приводятся в таблицах (Приложение 4). Причина зависимости t от P очевидна: чем выше доверительная вероятность, тем шире должен быть доверительный интервал с тем, чтобы можно было гарантировать попадание в него значения величины x. Поэтому с ростом P значения t возрастают. Зависимость t от f объясняется следующим образом. Поскольку 
– величина случайная, то в силу случайных причин ее значение может оказаться заниженным. В этом случае и доверительный интервал окажется более узким, и попадание в него значения величины x уже не может быть гарантировано с заданной доверительной вероятностью. Чтобы исключить подобную ошибку следует расширить доверительный интервал и для этого увеличить значение t – тем больше, чем менее надежно известно значение , то есть чем меньше число его степеней свободы. Поэтому с уменьшением f величина t возрастает. В практике физико-химических измерений обычно расчеты проводят для доверительной вероятности Р = 0,95 и реже для Р = 0,99 или 0,999, число измерений редко превышает 10 – 15.
Если измерение повторяется в других условиях, с другой аппаратурой, по другой методике или другим экспериментатором, вероятность получения того же результата мала. Действительно, в двух сериях измерений могут получиться разные ошибки и разные результаты. Часто важно знать, есть ли разница между значениями дисперсии и средних значений измеряемой величины или на языке статистики, принадлежат ли выборки одной и той же генеральной совокупности. Для сравнения двух выборочных дисперсий отклонений служит критерий Фишера (уравнение (8)).
Рассмотрим пример расчета критерия Фишера. Два фармацевта при определении концентрации уксусной кислоты получили приведенные ниже результаты.
| с 1, моль/л | с 2, моль/л | с 3, моль/л | с 4, моль/л |  ,
моль/л
| s2 ∙108 (моль/л)2 | |
| фармацевт А | 0,1009 | 0,1006 | 0,1004 | 0,1010 | 0,10073 | 2,74 |
| фармацевт Б | 0,1003 | 0,1003 | 0,1005 | 0,1004 | 0,10038 | 0,924 |
Значимо ли различие между дисперсиями результатов, полученных разными фармацевтами?
Поскольку 
, то 
Критическое значение F при уровне значимости 0,05 и при трех степенях свободы для каждой из дисперсий равно 9,28. Рассчитанное по экспериментальным данным значение F оказалосьменьше табличного. Это означает, что при доверительной вероятности 95% разница между дисперсиями двух серий результатов незначима.
Для того чтобы выяснить, значима ли разница между двумя средними значениями измеряемой величины в двух сериях измерений применяют критерий Стьюдента t:
 .
| (12) |
Значение t, рассчитанное по уравнению (12), следует сравнить с критическим значением при f = n 1 + n 2 – 2 степенях свободы и заданной доверительной вероятности.
Для рассмотренного выше примера, где
n А = 4, 
,
n Б = 4, 
,
критерий Стьюдента равен:
Число степеней свободы равно 4 + 4 – 2 = 6. В таблице (Приложение 4) находим, что t кр = 2,447 при доверительной вероятности 95%. Так как t < t кр, то это означает, что между средними значениями с вероятностью 95% имеется значимая разница.
Примеры решения задач
1. Для изучения ошибки работы рН-метра в кислой и щелочной средах проведены измерения рН в шести порциях буферного раствора I и в шести порциях буферного раствора II и получены следующие результаты:
| рН раствора I | 3,82 | 3,86 | 3,83 | 3,80 | 3,81 | 3,86 |
| рН раствора II | 9,18 | 9,13 | 9,15 | 9,18 | 9,16 | 9,14 |
Рассчитайте дисперсии измерений рН этих растворов. Значимо ли различие между дисперсиями?
Решение:
По формуле (2) рассчитываем среднее арифметическое значение рН растворов:
Выборочные дисперсии отдельных измерений рассчитываем по формуле (3):
Отношение дисперсий определяем по формуле (8):
Это значение меньше критического значения критерия Фишера 
, что позволяет считать различие между дисперсиями незначимым.
2. В результате кислотно-основного титрования были получены следующие объемы титранта (мл):
| № измерения | |||||||
| V, мл | 15,3 | 15,3 | 15,2 | 15,3 | 15,1 | 15,4 | 15,3 |
Рассчитайте среднее арифметическое значение измеряемой величины, стандартное отклонение отдельного измерения, стандартное отклонение среднего и доверительный интервал.
Решение:
Используя уравнение (2), рассчитаем среднее арифметическое значение измеряемой величины – объема титранта:
.
Рассчитываем стандартное отклонение отдельного измерения по уравнению (7):
.
Стандартное отклонение среднего значения случайной величины определяется по формуле (4) и равна:
Для расчета доверительного интервала необходимо определить по формуле (9) его полуширину: 
где 
– критическое значение критерия Стьюдента при f = n – 1 = 7 – 1 = 6, определенное по таблице (Приложение 4) для вероятности 95%.
Доверительный интервал для вероятности 95% определяется неравенством (11) и равен: 
.
|
|
|
