 |
Расчет коэффициентов прямой
|
|
|
|
В физико-химических исследованиях и в расчетных задачах часто возникает необходимость определения коэффициентов прямой y=ax+b. Коэффициенты а и b могут быть найдены разными способами:
1) по графику методом экстраполяции или интерполяции при х = 0 определяют коэффициент b в уравнении прямой, а затем по формуле
 , ,
| (16) |
используя координаты yi и xi любой точки, лежащей на прямой, рассчитывают коэффициент а;
2) по двум точкам на прямой рассчитывают коэффициент а,
 , ,
| (17) |
а затем по формуле
| b= yi – axi | (18) |
вычисляют коэффициент b;
3) методом наименьших квадратов.
Первый способ определения коэффициентов прямой используется в том случае, когда точка х = 0 расположена в пределах рисунка (рис. 23). По графику определяем значение коэффициента b, как ординату точки, лежащей на прямой, у которой абсцисса равна 0 (х = 0). b = 1. Далее выбираем любую точку на прямой (например, точку 1), определяем ее координаты и по уравнению (16)рассчитываем значение коэффициента а:


Рис. 23. Вид графика, по которому удобно определять коэффициенты прямой y=ax+b первым способом
В том случае, когда точка х = 0 расположена за пределами рисунка, используют второй способ определения коэффициентов прямой y=ax+b (рис. 24). Вначале выбираем две любые точки, лежащие на прямой (например, точки 1 и 2) и определяем их координаты:
(·)1 (0,8; 2); (·)2 (2,4; 4).
Затем рассчитываем угловой коэффициент по формуле (17):

Далее по уравнению (18) рассчитываем значение коэффициента b:
b= y1 – ax1 = 2 – 1,25 · 0,8 = 1.

Рис. 24. Вид графика, по которому удобно определять коэффициенты прямой y=ax+b вторым способом
В расчетах, требующих высокой точности нахождения коэффициентов прямой, следует пользоваться третьим способом – методом наименьших квадратов (МНК).
|
|
|
МНК предназначен для исключения неопределенности рассчитываемых коэффициентов, он позволяет провести единственным образом прямую и рассчитать единственный набор коэффициентов. Данный метод применим как для линейных, так и нелинейных зависимостей. Линия (в частном случае – прямая) проводится по набору экспериментальных точек методом наименьших квадратов таким образом, чтобы сумма квадратов отклонений ординат экспериментальных точек от расчетных, лежащих на прямой, была минимальной. Теория этого метода позволяет получить для расчета коэффициентов уравнения прямой yi = a хi + b:
 , ,
| (19) |
 , ,
| (20) |
где n – число экспериментальных точек; хi и yi – координаты i -той точки.
Суммы в выражениях (19) и (20) вычисляются по всем значениям от 1 до n. Расчеты проводим, занося промежуточные результаты в таблицу. Рассмотрим пример.
| № | хi | yi | хi2 | хi yi |
| 2,0 | 5,6 | 4,00 | 11,20 | |
| 3,5 | 7,3 | 12,25 | 12,55 | |
| 4,7 | 8,3 | 22,09 | 39,01 | |
| 5,4 | 8,8 | 29,16 | 47,52 | |
| 6,5 | 9,8 | 42,25 | 63,70 | |
| 8,0 | 11,2 | 64,00 | 89,60 | |
| 9,2 | 12,3 | 84,64 | 113,16 | |
| 10,0 | 13,3 | 100,00 | 133,00 | |

| 
| 
| 
|
Используя табличные данные, по формулам (19) и (20) рассчитаем коэффициенты:


уравнения прямой
 .
.
Для повышения точности и облегчения расчетов в настоящее время данные расчеты проводят в электронных таблицах Excel, где уже заложен метод наименьших квадратов.
Рассмотрим расчет коэффициентов прямой а и b с помощью электронных таблиц Excel. Вносим в поле таблицы значения х и y (рис. 26). На главной панели окна активируем иконку «мастер диаграмм», выбираем тип диаграммы – точечная (рис. 27). Далее на области построения диаграммы появляются точки, координаты которых заданы в таблице (в условии задания) (рис. 28). Затем предлагается озаглавить полученную графическую зависимость и оси координат (рис. 29). После построения графика, необходимо добавить линию тренда (рис. 30), установив ее формат (рис. 31), и уравнение (рис. 32), в которое и будут входить коэффициенты а и b уравнения прямой (рис. 33). В уравнении прямой можно выбрать форму представления значений коэффициентов (числовой, экспоненциальный), а также число десятичных знаков после запятой (рис. 25).
|
|
|

Рис. 25. Расчет коэффициентов прямой методом наименьших квадратов с использованием таблиц Excel

|
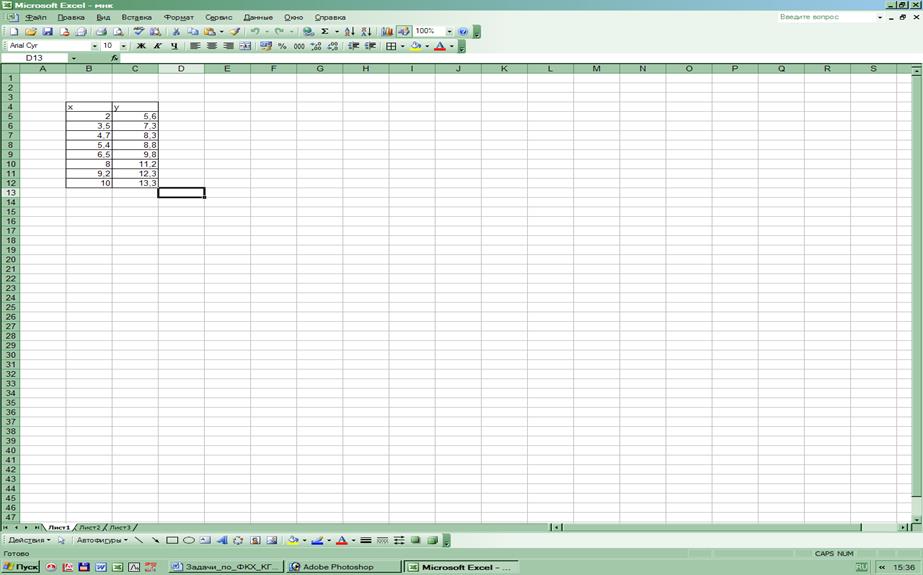
Рис. 26. Расчет коэффициентов прямой методом МНК: исходные данные

|

|
|


|

Рис. 27. Расчет коэффициентов прямой методом МНК: мастер диаграмм

|

Рис. 28. Расчет коэффициентов прямой методом МНК: вывод данных на область построения

|


|
|


Рис. 29. Расчет коэффициентов прямой методом МНК: название диаграммы

|

|

Рис. 30. Расчет коэффициентов прямой методом МНК: построение графической зависимости построение линии тренда

|
|

Рис. 31. Расчет коэффициентов прямой методом МНК: формат линии тренда


|

|
|

Рис. 32. Расчет коэффициентов прямой методом МНК: вывод уравнения прямой

|

Рис. 33. Расчет коэффициентов прямой методом МНК: уравнение прямой
|
|
|


