 |
Задачи и упражнения для самостоятельного решения
|
|
|
|
1. При определении вязкости растворов желчных кислот получили следующие результаты:
| № измерения | |||||
| n (число капель) |
Определите среднее арифметическое значение числа капель.
(Ответ: 123,4)
2. Фармацевт сделал пять измерений рН раствора и получил следующие значения: 3,87; 3,89; 3,86; 3,88 и 3,86. Определите среднее арифметическое значение рН, среднее квадратичное отклонение отдельного измерения, среднее квадратичное отклонение среднего и доверительный интервал для среднего арифметического.
(Ответ: 3,87; 0,013; 0,051; 3,87 – 0,141< μ <3,87 + 0,141)
3. При измерении константы скорости некоторой реакции в пяти опытах получены значения 0,100; 0,105; 0,101; 0,108 и 0,100 с–1. После изменения методики в шести дополнительных опытах в тех же условиях были получены значения 0,097; 0,099; 0,098; 0,095; 0,096 и 0,097 с–1. Значимо ли различие между дисперсиями в двух сериях измерений?
(Ответ: разница между дисперсиями двух серий результатов значима)
4. Два фармацевта по однотипной методике проводили физико-химическое исследование природных сорбентов. После титрования фильтрата раствором щелочи получили следующие результаты, V (мл):
| фармацевт 1 | 21,6 | 21,1 | 21,4 | 21,7 | 21,9 | |||
| фармацевт 2 | 22,0 | 20,6 | 21,3 | 20,4 | 21,2 | 21,5 | 21,4 | 20,9 |
Можно ли считать значимым различие между средними значениями объемов титранта, полученными двумя фармацевтами?
(Ответ: разница между дисперсиями двух серий результатов значима)
Ошибки измерений
Источники ошибок измерений могут быть самыми разнообразными: ошибка измерительных приборов, неопытность экспериментатора, расчет по формулам. По источникам ошибки измерений подразделяют на грубые, систематические и случайные.
|
|
|
Грубые ошибки или промахи вызваны нарушениями основных условий измерения, несоблюдением методики проведения эксперимента или небрежностью в работе. Результат, содержащий грубую ошибку, резко отличается по значению от остальных измерений. Грубые ошибки устраняются при повторном проведении эксперимента с соблюдением всех требуемых условий, предусмотренных методикой.
Систематические ошибки могут быть вызваны неполадками в работе измерительных приборов (приборные ошибки), обусловлены несовершенством метода измерений (методические ошибки), при использовании неточно откалиброванной посуды, при титровании раствором с неправильно установленным титром или загрязнения реагентов. Систематическая ошибка влияет на среднее серии измерений, вызывая завышение или занижение каждого результата. Например, смещен ноль шкалы прибора и все результаты измерений отличаются от действительных на величину этого смещения. Систематические ошибки могут быть устранены введением соответствующих поправок в результаты измерений.
Случайные ошибки измерений неизбежны. Случайные ошибки возникают вследствие неспособности экспериментатора полностью контролировать условия (изменение температуры, давления, влажности воздуха) или абсолютно воспроизводимо считывать результаты измерений со шкалы прибора. Они могут привести к завышению или занижению результатов и повлиять на среднее нескольких результатов, но при увеличении числа результатов положительные ошибки стремятся компенсировать отрицательные, а среднее стремится к истинному значению.
Рассмотрим систематическую и случайную ошибки, которые могут возникнуть при проведении обычного эксперимента, например, при титровании фильтрата (водного раствора уксусной кислоты), полученного после адсорбции активированным углем, стандартным раствором гидроксида натрия. Это сравнительно простой эксперимент; многие другие эксперименты включают большее число стадий.
|
|
|
Вероятность возникновения случайной и систематической ошибки возможна на каждом этапе эксперимента. Например, при измерении объема уксусной кислоты, взятого для титрования. При отборе каждой пробы одной и той же пипеткой возникает систематическая ошибка, если только средний объем выливающейся жидкости не будет точно таким, каким его считают. Пипетки градуируют при изготовлении, но полностью полагаться на точность градуировки нельзя. Для пипетки высшего качества объемом 25 мл эта цифра может быть дана с ошибкой ±0,025 мл при температуре (обычно 25 ºС), при которой пипетка, по мнению изготовителя, будет использоваться. Соответствующая относительная ошибка равна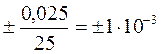 
, или ±0,1%. Результат может отклоняться на 0,1% от истинного значения в том или другом направлении. Систематическая ошибка будет значительно больше, если пипеткой пользоваться неправильно (неверно устанавливая мениск или спуская жидкость слишком быстро), если подвергали ее действию очень концентрированных кислот или щелочей, разъедавших ее внутри, или нагревая, после чего могут потребоваться недели или месяцы, чтобы вернуть ее к первоначальному объему. Пипетку невозможно каждый раз заполнить точно до одного и того же уровня и вылить из нее раствор совершенно одинаково, что также приводит к появлению случайной ошибки. Даже самые аккуратные исполнители, работающие в самых лучших условиях, не смогли бы получить абсолютно идентичные объемы проб для последовательных титрований. Разница в этих объемах зависит от квалификации и аккуратности экспериментатора, она может достигать 0,1 или 0,2 мл или не превышать примерно 0,003 мл. Если не контролировать изменения температуры отбираемого пипеткой раствора, случайная ошибка возрастает, потому что при увеличении температуры увеличивается объем пипетки, а также увеличивается объем раствора. Для пипетки из мягкого стекла и разбавленного водного раствора повышение температуры на 1ºС приводит к увеличению ее объема на 0,003% и уменьшению концентрации раствора на 0,026% и, таким образом, к уменьшению количества отобранного вещества на 0,023%.
|
|
|
Ошибки можно допустить на любом этапе работы, для уменьшения систематической и случайной ошибки нужна обычно несколько большая тщательность. Изменение какой-либо детали методики может повлиять и на систематическую и на случайную ошибку.
Абсолютная ошибка Δ хi – это значение разности между результатом измерения хi и средним арифметическим значением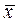 
, которая тем ближе к истинному значению измеряемой величины μ, чем больше проведено измерений:
 .
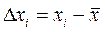| (13) |
Абсолютную ошибку выражают в единицах измеряемой величины, то есть Δ х имеет размерность ту же, что и х.
Относительная ошибка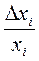 
– это отношение абсолютной ошибки Δ хi к полученному значению измеряемой величины хi:
 .
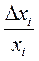| (14) |
Относительная ошибка – безразмерная величина, она может быть выражена в процентах.
Правильность результата, то есть наличие систематической ошибки, легко проверить, пользуясь справочными или паспортными данными химической посуды и оборудования. Это позволяет находить поправки, с помощью которых можно получить результаты, не содержащие систематической ошибки.
Случайные ошибки, в отличие от систематических исключить нельзя, но, увеличивая количество измерений, можно уменьшить среднее значение случайной ошибки и, в итоге, повысить точность результата измерения.
Измерения могут быть прямые и косвенные.
Ошибки прямых измерений возникают в том случае, если величина измеряется непосредственно без расчета по формуле. Виды ошибок, возникающих при прямых измерениях, рассмотрены в разделе 1 «Элементы теории вероятностей и математической статистики».
Ошибки косвенных измерений. Косвенными называют такие измерения, при которых вначале проводят прямые измерения некоторых величин (х 1, х 2, …), а затем, используя эти значения, рассчитывают по формуле другую величину y.
Результаты большинства физико-химических определений представляют собой итоги косвенных измерений, поскольку даже простой расчет массовой доли компонента в пробе проводится по формуле:
 ,
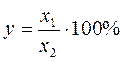| (15) |
где y – массовая доля компонента; x 1 – масса компонента, найденная в ходе анализа; x 2 – исходная навеска пробы.
|
|
|
Если расчеты по формуле включают в себя несколько измеряемых величин, то необходимо учитывать относительную и абсолютную ошибку каждой измеряемой величины. Например, при определении молярной массы вещества М по увеличению температуры кипения Δ Т к разбавленного раствора используют формулу:
,
где Е – эбулиоскопическая постоянная; g – масса растворенного вещества; G – масса растворителя. Если считать, что величина Е – справочная величина и является точной, то ошибка в расчете молярной массы Δ М будет функцией ошибок непосредственно измеряемых величин Δ g, Δ G и Δ(Δ Т к). В том случае, когда ошибки не являются случайными и в правой части формулы есть только деление и умножение величин, относительная ошибка рассчитываемой величины будет равна сумме относительных ошибок величин, входящих в правую часть:
,
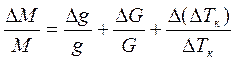то есть равна сумме относительных ошибок измеренных величин.
Примерами ошибок, которые не являются случайными, могут быть максимальные ошибки, возникающие при отсчете объема раствора по бюретке или пипетке, при измерении температуры, определении рН с помощью рН-метра и в других аналогичных случаях. Такие ошибки называются иногда приборными. Все методы, в которых используются градуировочные графики, эталоны и стандарты, приводят, в конечном счете, к косвенной оценке количеств определяемого компонента.
По ходу последовательных стадий эксперимента и соответствующих им расчетов погрешности накапливаются, и любой пересчет, использующий ранее полученные значения, может сопровождаться лишь возрастанием ошибок.
Примеры решения задач
Для нахождения ошибки рН-метра в кислой и щелочной средах проведены измерения рН стандартных буферных растворов:
| № | ||||||
| рН раствора I | 3,82 | 3,86 | 3,83 | 3,80 | 3,81 | 3,86 |
Истинное значение рН равно 3,80. Рассчитайте среднее арифметическое значение рН, абсолютную ошибку между результатом измерения и средним арифметическим значением, абсолютную ошибку измерения рН между средним и истинным значением рН.
Решение:
Среднее арифметическое значение рН раствора равно (формула (2)):
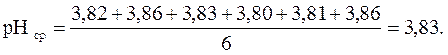
Абсолютная ошибка между результатом измерения и средним арифметическим значением определяется по формуле (13) и равна:
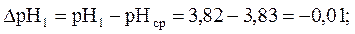
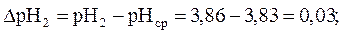
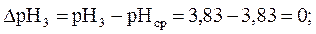
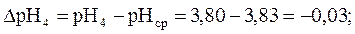
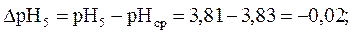
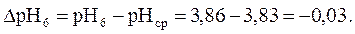
Абсолютная ошибка измерения рН между средним и истинным значением рН равна:
|
|
|
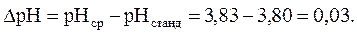
