Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.

В) Числовая прямая

Рассмотрим числовую прямую (рис. 6):

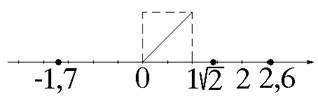
Рис. 6

Рассмотрим множество рациональных чисел

Каждое рациональное число изображается некоторой точкой на числовой оси. Так, на рисунке отмечены числа .

Докажем, что .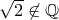

Доказательство. Пусть существует дробь : . Мы вправе считать эту дробь несократимой. Так как , то — число четное: — нечетное. Подставляя вместо его выражение, найдем: , откуда следует, что — четное число. Получили противоречие, которое доказывает утверждение.

Итак, не все точки числовой оси изображают рациональные числа. Те точки, которые не изображают рациональные числа, изображают числа, называемые иррациональными.

Любое число вида , , является либо целым, либо иррациональным.

Числовые промежутки

Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.

Неравенство, задающее числовой промежуток	Обозначение числового промежутка	Название числового промежутка	Читается так:
a ≤ x ≤ b	[ a; b ]	Числовой отрезок	Отрезок от a до b
a < x < b	(a; b)	Интервал	Интервал от a до b
a ≤ x < b	[ a; b)	Полуинтервал	Полуинтервал от a до b, включая a.
a < x ≤ b	(a; b ]	Полуинтервал	Полуинтервал от a до b, включая b.
x ≥ a	[ a; + ∞)	Числовой луч	Числовой луч от a до плюс бесконечности
x > a	(a; + ∞)	Открытый числовой луч	Открытый числовой луч от a до плюс бесконечности
x ≤ a	(- ∞; a ]	Числовой луч	Числовой луч от минус бесконечности до a
x < a	(- ∞; a)	Открытый числовой луч	Открытый числовой луч от минус бесконечности до a

Представим на координатной прямой числа a и b, а также число x между ними.

Множество всех чисел, отвечающих условию a ≤ x ≤ b, называется числовым отрезком или просто отрезком. Обозначается так: [ a; b ]-Читается так: отрезок от a до b.

Множество чисел, отвечающих условию a < x < b, называется интервалом. Обозначается так: (a; b)

Читается так: интервал от a до b.

Множества чисел, отвечающих условиям a ≤ x < b или a < x ≤ b, называются полуинтервалами. Обозначения:

Множество a ≤ x < b обозначается так:[ a; b),-читается так: полуинтервал от a до b, включая a.

Множество a < x ≤ b обозначается так:(a; b ],-читается так: полуинтервал от a до b, включая b.

Теперь представим луч с точкой a, справа и слева от которой - множество чисел.

Множество чисел справа от точки a, отвечающих условию x ≥ a, называется числовым лучом.

Обозначается так: [ a; + ∞)-Читается так: числовой луч от a до плюс бесконечности.

Множество чисел справа от точки a, отвечающих неравенству x > a, называется открытым числовым лучом.

Обозначается так: (a; + ∞)-Читается так: открытый числовой луч от a до плюс бесконечности.

Множество чисел слева от точки a, отвечающих условию x ≤ a, называется числовым лучом от минус бесконечности до a.

Обозначается так:(- ∞; a ]-Читается так: числовой луч от минус бесконечности до a.

Множество чисел слева от точки a, отвечающих неравенству x < a, называется открытым числовым лучом от минус бесконечности до a.

Обозначается так: (- ∞; a)-Читается так: открытый числовой луч от минус бесконечности до a.

Множество действительных чисел изображается всей координатной прямой. Его называют числовой прямой. Обозначается она так: (- ∞; + ∞)

3)Линейные уравнения и неравенства с одной переменной,их решения:

Равенство, содержащее переменную, называют уравнением с одной переменной, или уравнением с одним неизвестным. Например, уравнением с одной переменной является равенство 3(2х+7)=4х-1.

Корнем или решением уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство. Например, число 1 является решением уравнения 2х+5=8х-1. Уравнение х2+1=0 не имеет решения, т.к. левая часть уравнения всегда больше нуля. Уравнение (х+3)(х-4) =0 имеет два корня: х1= -3, х2=4.

Решить уравнение — значит найти все его корни или доказать, что корней нет.

Уравнения называются равносильными, если все корни первого уравнения являются корнями второго уравнения и наоборот, все корни второго уравнения являются корнями первого уравнения или, если оба уравнения не имеют корней. Например, уравнения х-8=2 и х+10=20 равносильны, т.к. корень первого уравнения х=10 является корнем и второго уравнения, и оба уравнения имеют по одному корню.

При решении уравнений используются следующие свойства:

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получите уравнение, равносильные данному.

Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Уравнение ах=b, где х – переменная, а и b – некоторые числа, называется линейным уравнением с одной переменной.

Если а¹0, то уравнение имеет единственное решение .

Если а=0, b=0, то уравнению удовлетворяет любое значение х.

Если а=0, b¹0, то уравнение не имеет решений, т.к. 0х=b не выполняется ни при одном значении переменной.
Пример 1. Решить уравнение: -8(11-2х)+40=3(5х-4)

Раскроем скобки в обеих частях уравнения, перенесем все слагаемые с х в левую часть уравнения, а слагаемые, не содержащие х, в правую часть, получим:

16х-15х=88-40-12

х=36

Ответ: 36.

Пример 2. Решить уравнения:

3х2-5х=0;

х3-2х2-98х+18=0;

х2+7х+12=0.

Эти уравнения не являются линейными, но покажем, как можно решать такие уравнения.

3х2-5х=0; х(3х-5)=0. Произведение равно нулю, если один из множителей равен нулю, получаем х1=0; х2= .

Ответ: 0; .

Разложить на множители левую часть уравнения:

х2(х-2)-9(х-2)=(х-2)(х2-9)=(х-2)(х-3)(х-3), т.е. (х-2)(х-3)(х+3)=0. Отсюда видно, что решениями этого уравнения являются числа х1=2, х2=3, х3=-3.

с) Представим 7х, как 3х+4х, тогда имеем: х2+3х+4х+12=0, х(х+3)+4(х+3)=0, (х+3)(х+4)=0, отсюда х1=-3, х2=- 4.

Ответ: -3; - 4.
Пример 3. Решить уравнение: ½х+1ç+½х-1ç=3.

Напомним определение модуля числа: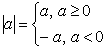

Например: ½3½=3, ½0½=0, ½- 4½= 4.

В данном уравнении под знаком модуля стоят числа х-1 и х+1. Если х меньше, чем –1, то число х+1 отрицательное, тогда ½х+1½=-х-1. А если х>-1, то ½х+1½=х+1. При х=-1 ½х+1½=0.

Таким образом,

Аналогично

а) Рассмотрим данное уравнение½х+1½+½х-1½=3 при х£-1, оно равносильно уравнению -х-1-х+1=3, -2х=3, х= , это число принадлежит множеству х£-1.

b) Пусть -1 < х £ 1, тогда данное уравнение равносильно уравнению х+1-х+1=3, 2¹3 уравнение не имеет решения на данном множестве.

с) Рассмотрим случай х>1.

х+1+х-1=3, 2х=3, х= . Это число принадлежит множеству х>1.

Ответ: х1=-1,5; х2=1,5.
Пример 4. Решить уравнение:½х+2½+3½х½=2½х-1½.

Покажем краткую запись решения уравнения, раскрывая знак модуля «по промежуткам».

-2 0 1 х

х £-2, -(х+2)-3х=-2(х-1), - 4х=4, х=-2Î(-¥; -2]

–2<х£0, х+2-3х=-2(х-1), 0=0, хÎ(-2; 0]

0<х£1, х+2+3х=-2(х-1), 6х=0, х=0Ï(0; 1]

х>1, х+2+3х=2(х-1), 2х=- 4, х=-2Ï(1; +¥)

Ответ: [-2; 0]
Пример 5. Решить уравнение: (а-1)(а+1)х=(а-1)(а+2), при всех значениях параметра а.

В этом уравнении на самом деле две переменных, но считают х–неизвестным, а а–параметром. Требуется решить уравнение относительно переменной х при любом значении параметра а.

Если а=1, то уравнение имеет вид 0×х=0, этому уравнению удовлетворяет любое число.

Если а=-1, то уравнение имеет вид 0×х=-2, этому уравнению не удовлетворяет ни одно число.

Если а¹1, а¹-1, тогда уравнение имеет единственное решение .

Ответ: если а=1, то х – любое число;

если а=-1, то нет решений;

если а¹±1, то .

Б) Линейные неравенства с одной переменной.

Если переменной х придать какое-либо числовое значение, то мы получим числовое неравенство, выражающее либо истинное, либо ложное высказывание. Пусть, например, дано неравенство 5х-1>3х+2. При х=2 получим 5·2-1>3·2+2 – истинное высказывание (верное числовое высказывание); при х=0 получаем 5·0-1>3·0+2 – ложное высказывание. Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется решением неравенства. Решить неравенство с переменной – значит найти множество всех его решений.

Два неравенства с одной переменной х называются равносильными, если множества решений этих неравенств совпадают.

Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяем более простым равносильным ему неравенством и т.д.

Такие замены осуществляются на основе следующих утверждений.

Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.

Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному.

Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному.

Линейным называется неравенство вида ax+b>0 (соответственно ax+b<0, ax+b³0, ax+b£0), где а и b – действительные числа, причем а¹0. Решение этих неравенств основано на трех теоремах равносильности изложенных выше.

Пример 1. Решить неравенство: 2(х-3)+5(1-х)³3(2х-5).

Раскрыв скобки, получим 2х-6+5-5х³6х-15,

-3х-1³6х-15, -9х³-14, .

Ответ: .

Пример 2. Решить неравенство: .

Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства.

, далее последовательно получаем ; .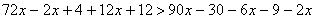

Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0>-55. Поэтому множеством его решений служит вся числовая прямая.

Ответ: (-¥; +¥).

Пример 3. Решить неравенство: ½х-1½<3.

На основании определения модуля данное неравенство запишем в виде совокупности двух систем неравенств

(1) (2)

решая эту совокупность получим (2), таким образом решением этого неравенства является промежуток (-2; 4).

Пример 4. Решить неравенство:½х+1½>2-х.

отсюда х>0,5 из первой системы, а вторая система – не имеет решения.
Ответ: (0,5; +¥)

4)Квадратные уравнения (полные и неполные),их решения:

Квадратное уравнение — уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.

Числа называются коэффициентами квадратного уравнения.

• называется первым коэффициентом;
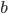• называется вторым коэффициентом;
• — свободным членом.

Приведенное квадратное уравнение — уравнение вида 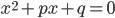, первый коэффициент которого равен единице ().

Если в квадратном уравнении коэффициенты 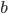и не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение 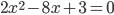. Если один из коэффициентов 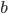или равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, .Значение неизвестного , при котором квадратное уравнение обращается в верное числовое равенство, называется корнем этого уравнения. Например, значение 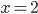является корнем квадратного уравнения , потому что 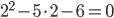или — это верное числовое равенство. Решить квадратное уравнение — это значит найти множество его корней.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: