 |
Исходная система уравнений допускает следующие тождественные преобразования:
|
|
|
|
1. 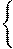 f1(x
f1(x  y)=C1;f2(x
y)=C1;f2(x  y)=C2
y)=C2 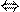
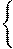 af1(x
af1(x  y)+bf2(x
y)+bf2(x  y)=aC1+bC2;f2(x
y)=aC1+bC2;f2(x  y)=C2
y)=C2
2. 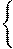 f1(x
f1(x  y)=C1;f2(x
y)=C1;f2(x  y)=C2
y)=C2 
 f1(x
f1(x  y)
y)  f2(x
f2(x  y)=C1
y)=C1  C2;f2(x
C2;f2(x  y)=C2
y)=C2
3.  f1(x
f1(x  y)=C1;f2(x
y)=C1;f2(x  y)=C2
y)=C2 
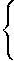 f2(x
f2(x  y)f1(x
y)f1(x  y)=C2/C1;f2(x
y)=C2/C1;f2(x  y)=C2
y)=C2
Замечание: Данные преобразования возможны, если a  =0 и C2
=0 и C2  =0.. Аналогично можно преобразовать и второе уравнение системы.
=0.. Аналогично можно преобразовать и второе уравнение системы.
Система линейных уравнений с двумя переменными. Система вида 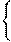 a1x+b1y=c1;a2x+b2y=c2
a1x+b1y=c1;a2x+b2y=c2  где a21+b21
где a21+b21  =0 и a22+b22
=0 и a22+b22  =0, называются системой двух линейных уравнений с двумя неизвестными.
=0, называются системой двух линейных уравнений с двумя неизвестными.
Система линейных уравнений:
- имеет единственное решение, если a2a1
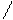 =b2b1;
=b2b1; - имеет бесконечное множество решений, если a2a1=b2b1=c2c1;
- не имеет решений, если a2a1=b2b1
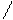 =c2c1.
=c2c1.
Решение системы линейных уравнений - метод последовательного исключения переменной:
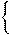 2x−3y=1;x+2y=4
2x−3y=1;x+2y=4 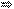
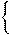 2(4−2y)−3y=1;x=4−2y
2(4−2y)−3y=1;x=4−2y 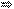
 8−4y−3y=1;x=4−2y
8−4y−3y=1;x=4−2y 
 y=1;x=2. Ответ: (2; 1)
y=1;x=2. Ответ: (2; 1)
С)Уравнение может содержать две переменных. Такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два уравнения, которыми можно манипулировать для нахождения общих решений. Говоря иначе, с помощью одного уравнения системы решается второе, а благодаря этому затем решаются все уравнения системы.
Способы решения системы уравнений первой степени.
Решение методом подстановки.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и выбираем для манипуляций.
Находим буквенно-числовое значение x:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
-3y = 2 – 2
-3y = 0
y = 0
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
Метод алгебраического сложения.
|
|
|
Пример №1:
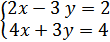
Решение:
Можно заметить, что в двух уравнениях присутствует одна и та же переменная: 3y, только с разными знаками. Следовательно, их можно алгебраически сложить и мы получим равносильную систему:
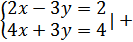
1) 6x = 6
x = 1
Итак, мы нашли значение первой переменной: x = 1. теперь подставляем это значение в любую из уравнений, чтобы найти значение второй переменной:
2) 
2  1 – 3y = 2
1 – 3y = 2
-3y = 0
y = 0
Получили: y = 0.
Ответ: (1; 0).
3) Метод графического решения.
Пример №1:
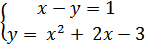
Решение:
Для начала перенесём переменную x в правую сторону, чтобы получить уравнение функции:
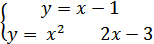
Теперь начертим графики полученных функций:
Функция №1:
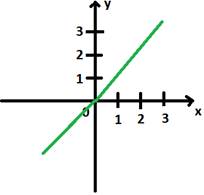
Функция №2:

Теперь найдём их пересечение:
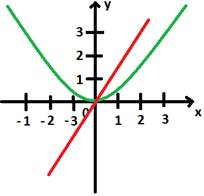
Ответ: (0; 0).
7)Числовая функция,способы задания:
числовая функция - это функция, области определения и значений которой являются подмножествами числовых множеств - как правило, множества действительных чисел
График функции
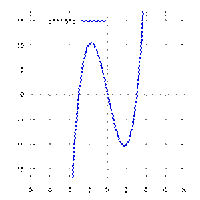 Фрагмент графика функции
Фрагмент графика функции 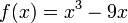
- Пусть дано отображение
 . Тогда его гра́фиком
. Тогда его гра́фиком 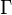 называется множество
называется множество
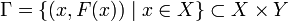 ,
,
где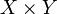 обозначает декартово произведение множеств
обозначает декартово произведение множеств 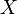 и
и  .
. - График непрерывной функции
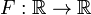 является кривой на двумерной плоскости.
является кривой на двумерной плоскости. - Графиком непрерывной функции
 является поверхность в трёхмерном пространстве.
является поверхность в трёхмерном пространстве.
Способы задания функции 
| Словесный | С помощью естественного языка | Игрек равно целая часть от х. | ||||||||||||||||||||||
| Аналитический | С помощью аналитической формулы | 
| ||||||||||||||||||||||
| Графический | С помощью графика | 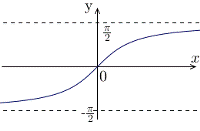 Фрагмент графика функции Фрагмент графика функции  . .
 Добавил Moisey Добавил Moisey
| ||||||||||||||||||||||
| Табличный | С помощью таблицы значений |
| ||||||||||||||||||||||
8)Область определения и область значения функции:
Область определения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).
Рассмотрим D (у) для 1.,2.,3.,4.
|
|
|
1. D (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. D (у)= (∞; +∞)//всё мн-во действит.чисел
3. D (у)= (∞; +∞)//всё мн-во действит.чисел
4. D (у)= [0; +∞)// мн-во неотрицат.чисел
Зависимая переменная (кот. мы обозначаем у) имеет название значение функции.
Область значения функции
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).
Рассмотрим Е (у) для 1.,2.,3.,4.
1. Е (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. Е (у)= [0; +∞)// мн-во неотрицат.чисел
3. Е (у)=(∞; +∞)//всё мн-во действит.чисел
4. Е (у)= [0; +∞)// мн-во неотрицат.чисел
|
|
|


