Формула суммы n-первых членов геометрической прогрессии

где, q ≠ 1

Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа .

Формула суммы членов бесконечно убывающей геометрической прогрессии:

где, q ≠ 1

Пример 1.

Задана геометрическая прогрессия 2,6,18,... Найти десятый член прогрессии и сумму её двенадцати первых членов.

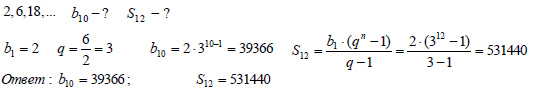
21)Приращение аргумента,приращение функции.их геометрическая изображение:

Понятия "приращение функции" и "приращение аргумента"

Допустим, х – некоторая произвольная точка, которая лежит в какой-либо окрестности точки х0. Приращением аргумента в точке х0 называется разность х-х0. Обозначается приращение следующим образом: ∆х.

• ∆х=х-х0.

Иногда эту величину еще называют приращением независимой переменной в точке х0. Из формулы следует: х = х0+∆х. В таких случаях говорят, что начальное значение независимой переменной х0, получило приращение ∆х.

Если мы изменяем аргумент, то и значение функции тоже будет изменяться.

• f(x) – f(x0) = f(x0 + ∆х) – f(x0).

Приращением функции f в точке x0, соответствующим приращению ∆х называется разность f(x0 + ∆х) – f(x0). Приращение функции обозначается следующим образом ∆f. Таким образом получаем, по определению:

• ∆f= f(x0 +∆x) – f(x0).

Иногда, ∆f еще называют приращением зависимой переменной и для обозначения используют ∆у, если функция была, к примеру, у=f(x).

Геометрический смысл приращения

Посмотрите на следующий рисунок.

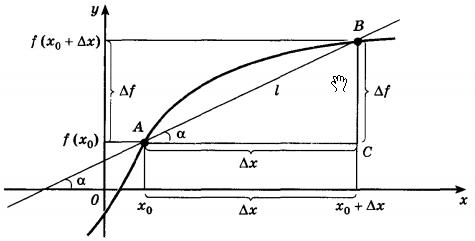
Как видите, приращение показывает изменение ординаты и абсциссы точки. А отношение приращения функции к приращению аргумента определяет угол наклона секущей, проходящей через начальное и конечное положение точки.

Рассмотрим примеры приращения функции и аргумента

Пример 1. Найти приращение аргумента ∆х и приращение функции ∆f в точке х0, если f(х) = х², x0=2 a) x=1.9 b) x =2.1

Воспользуемся формулами, приведенными выше:

a) ∆х=х-х0 = 1.9 – 2 = -0.1;

• ∆f=f(1.9) – f(2) = 1.9² – 2² = -0.39;

b) ∆x=x-x0=2.1-2=0.1;

• ∆f=f(2.1) – f(2) = 2.1² – 2² = 0.41.

Пример 2. Вычислить приращение ∆f для функции f(x) = 1/x в точке х0, если приращение аргумента равняется ∆х.

Опять же, воспользуемся формулами, полученными выше.

• ∆f = f(x0 + ∆x) – f(x0) =1/(x0-∆x) – 1/x0 = (x0 – (x0+∆x))/(x0*(x0+∆x)) = -∆x/((x0*(x0+∆x)).

 

22)Непрерывность функции в точке,на промежутке.свойства непрерывных функции.решение неравенств,методом интервалом:

В пунтке понятия о непрерывности функции вы познакомились с понятием непрерывности функции в точке. Если функция непрерывна в каждой точке некоторого промежутка I, то ее называют непрерывной на промежутке I (промежуток I называют промежутком непрерывности функции f). При переходе от одной точки этого промежутка к близкой ей точке значение функции меняется мало; график f на этом промежутке представляет собой непрерывную линию, о которой говорят, что ее можно «нарисовать, не отрывая карандаша от бумаги». (Так, во всяком случае, обстоит дело для непрерывных функций, изучаемых в школьном курсе.)

Как было показано в пункте правила вычисления производных, функция, дифференцируемая в точке x₀, непрерывна в этой точке. Все дробно-рациональные и основные тригонометрические функции дифференцируемы во всех точках своих областей определения. Следовательно, эти функции и непрерывны в каждой из этих точек.

Например, из дифференцируемости функции f (х) = x² на всей прямой, а функции f(x) = 1/x на промежутках (—∞;0) и (0;+∞) вытекает непрерывность этих функций на соответствующих промежутках.

Отметим следующее свойство непрерывных функций:

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: