 |
Свойства показательной функции
|
|
|
|
| Свойства показательной функции | y = a x, a > 1 | y = a x, 0< a < 1 |
| 
| |
| 2. Область значений функции | 
| |
| 3.Промежутки сравнения с единицей | при x > 0, a x >1 | при x > 0, 0< a x < 1 |
при x < 0, 0< a x < 1 
| при x < 0, a x >1 | |
| 4. Чётность, нечётность. | Функция не является ни чётной, ни нечётной (функция общего вида). | |
| 5.Монотонность. | монотонно возрастает на R | монотонно убывает на R |
| 6. Экстремумы. | Показательная функция экстремумов не имеет. | |
| 7.Асимптота | Ось O x является горизонтальной асимптотой. | |
8. При любых действительных значениях x и y; 
| 
|
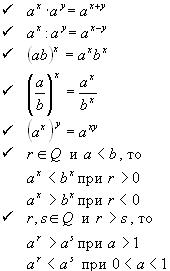
Показательная функция.
Функция вида y = ax, в которой a - положительное (постоянное) число, называют показательной функцией. Аргумент x принимает любые действительные значения; значениями функции обычно рассматривают только положительные числа, потому что иначе мы получаем многозначную функцию. Например, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i. (Корень 4ой степени из 81, где i2 = -1)
Так как значениями функции обычно рассматривают только положительные числа, рассматриваем в качестве значения только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии,параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 < a < 1 – убывает.
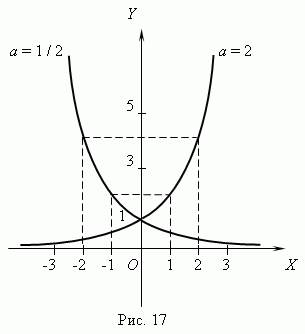
Основные характеристики и свойства показательной функции:
- область определения функции: - бесконечночть < x < + бесконечночть (т.e. x R);
область значений: y > 0;
- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;
- функция неограниченная, всюду непрерывная, непериодическая;
|
|
|
- нулей функция не имеет.
13)Понятие логарифма чисел.Общие свойства логарифмов.Формула перехода от одного основания логарифмов к другому:
Понятие логарифма
Ключевые слова: логарифм, степень, основание логарифма, логарифмическое число, десятичный логарифм, натуральный логарифм, основное логарифмическое тождество.
Логарифмом числа b по основанию a (b > 0, a > 0, a 
=1 ) называют показатель степени, в который нужно возвести число a, чтобы получить число b:
alogab=b
Это равенство, выражающее определение логарифма, называется основным логарифмическим тождеством.
Равенство logab=x означает, что ax=b.
Из определения логарифма получаются следующие важные равенства: loga1=0 
logaa=1.
Эти тождества следуют из равенств a0=1 a1=a.
Логарифм по основанию 10 имеет специальное обозначение log10b=lgb и называется десятичным логарифмом.
Логарифм по основанию e имеет в математике большое значение. Число e приблизительно равно 2,71, однако само число e является иррациональным.
Для логарифма по этому основанию также существует специальное обозначение logeb=lnb и название натуральный логарифм.
Среди свойств числа e, в частности, можно отметить следующее: касательная к графику функции y = ex в точке (0; 1) образует с осью абсцисс угол 45°.
Свойства логарифмов
Ключевые слова: логарифм, свойства логарифмов, формула перехода к новому основанию.
Из определения логарифма вытекают следующие его свойства. Пусть a > 0, a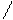 
= 0. Тогда:
- Если x > 0 и y > 0, то logax
y=logax+logay.
Например, log214=log2(2 7)=log22+log27=1+log27.
- Если x > 0 и y > 0, то logayx=logax−logay.
Например, loga0 
4=log552=log52−log55=log52−1.
- Если x > 0, то logaxp=plogax.
Например, log249=log272=2log27, log3 
45=log3541=41log35.
- Если b > 0, b 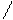= 1, x > 0, то logax=logbxlogba.
Например, log35=log73log75. Эта формула называется формулой перехода к новому основанию.
- Если x > 0, то logamxn=nm logax.
Например, log94=log3222=22 log32=log32, log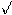 
5(53)−23=log521(53)−23=21−23log553=−3(log53−log55)=−3(log53−1)
|
|
|
|
|
|
