Решение неполных квадратных уравнений

ax² + bx = 0, a≠0, b≠0

Пусть неполное квадратное уравнение имеет вид , где a ≠ 0; b≠ 0. В левой части этого уравнения есть общий множитель .

1. Вынесем общий множитель за скобки.

Мы получим . Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем или 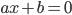. Таким образом, данное уравнение эквивалентно двум уравнениям:

2. Решаем получившуюся систему уравнений.

Решив эту систему, мы получим и . Следовательно, данное квадратное уравнение имеет два корня и .

Пример 1.

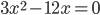
Разложим левую часть уравнения на множители и найдем корни:

Ответ: 0; 4.

ax² + c = 0, a≠0, с≠0

Для решения данного неполного квадратного уравнения выразим .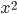

При решении последнего уравнения возможны два случая:

если , то получаем два корня:

если , то уравнение во множестве действительных числе не имеет решений.

Пример 2.

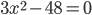
Таким образом, данное квадратное уравнение имеет два корня и

ax² = 0, a≠0

Разделим обе части уравнения на , мы получим , . Таким образом, данное квадратное уравнение имеет один корень . В этому случае говорят, что квадратное уравнение имеет двукратный корень .

Решение полного квадратного уравнения

Найдем решение полного квадратного уравнения ax² + bx + c = 0.

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения называется выражение b² — 4ac.

При решении уравнения с помощью дискриминанта возможны три случая:

1. D > 0. Тогда корни уравнения равны:

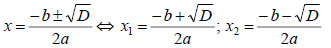
2. D = 0. В данном случае решение даёт два двукратных корня:

3. D < 0. В этом случае уравнение не имеет решения.

5)Квадратные неравенства,решения.

Квадратное неравенство — это неравенство вида: . Вместо знака «меньше» может быть знак «больше», «больше, либо равно», «меньше, либо равно».

Алгоритм решения квадратного неравенства следующий:

1)Приводим первоначальное неравенство к уравнению .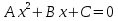

2)Находим корни этого уравнения.

- Допустим, корней уравнения нет. Тогда и множество решений исходного неравенства пустое.

- Пусть теперь квадратное уравнение имеет единственный корень . Тогда решение неравенства сводится к выбору промежутка значений, как в линейных неравенствах.

- Если квадратное уравнение имеет 2 корня 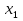и 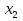(), то принцип определения промежутков тот же, но так как числовая прямая теперь разбита на 3 части, то для верного выбора промежутка надо пользоваться следующим правилом:

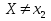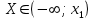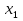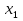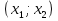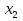Выбираем, как и прежде произвольное значение , . Определяем знак выражения при этом значении. Пусть . Тогда, если – корень нечётной кратности (то есть при нахождении корней квадратного уравнения нашлось нечётное количество одинаковых корней ), то на промежутке выражение будет иметь знак, отличный от знака на . Допустим, корень имеет чётную кратность, тогда на интервале это выражение будет иметь знак такой же, как и на .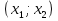

На графике разными цветами показаны интервалы, на которых выражение имеет разные знаки.

Ещё проще понять смысл выбора промежутка можно, построив график функции, задаваемой квадратным уравнением .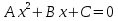

Тогда видно, что график лежит выше оси абсцисс, то есть 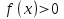, на интервале . А отрицателен график, 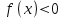, на промежутке .

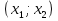У=Ах2+Вх+С.

6)Система двух линейных уравнений с двумя переменными.Их решение(подстановки,способалгебраического сложения,графический способ):

Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1.

Линейное уравнение можно представить

в общей форме:

в канонической форме: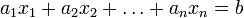

Система уравнений с двумя переменными: 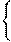f1(x y)=C1;f2(x y)=C2

Решением системы уравнений является пара чисел (a, b), при подстановке которой в исходную систему получаются верные тождества: 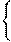f1(a b) C1;f2(a b) C2

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: