 |
Правила действий со степенями
|
|
|
|

| 
|

| 
|

| 
|

| 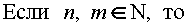
|

| 
|

| |

|
Действия над степенями производятся по нижеследующим правилам:

 (1)
(1)
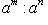
 (2)
(2)

 (3)
(3)

 (4)
(4)

 (5)
(5)
11)Степенная функция,ее общий вид (уметь строить график и описать свойства степенной функции при n=1; 2,3; -1; -2;1/2;1/3.):
СТЕПЕННАЯ ФУНКЦИЯ
Степенная функция - функция вида  , где
, где  - заданное число, называемое показателем степени. Иногда степенной функцией называется функция несколько более общего вида
- заданное число, называемое показателем степени. Иногда степенной функцией называется функция несколько более общего вида  .
.
Многие функциональные зависимости выражаются через степенную функцию. Например, объем куба 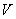 есть степенная функция от
есть степенная функция от  (длины его ребра):
(длины его ребра):  ; период
; период  колебаний математического маятника пропорционален длине маятника
колебаний математического маятника пропорционален длине маятника  в степени
в степени  , а именно
, а именно  . Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление
. Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление  и объем
и объем 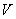 связаны формулой
связаны формулой  (для воздуха, например,
(для воздуха, например,  ). Заметим, что в двух последних случаях показатель не является целым числом.
). Заметим, что в двух последних случаях показатель не является целым числом.
При любом показателе степени  показательная функция
показательная функция  определена во всяком случае на положительной полуоси. Свойства степенной функции различны в зависимости от значения показателя степени. Если
определена во всяком случае на положительной полуоси. Свойства степенной функции различны в зависимости от значения показателя степени. Если  - натуральное число
- натуральное число  , то функция
, то функция  определена на всей числовой оси, обращается в нуль при
определена на всей числовой оси, обращается в нуль при  , четная при четном
, четная при четном  и нечетная при
и нечетная при  нечетном, неограниченно возрастает при безграничном возрастании аргумента
нечетном, неограниченно возрастает при безграничном возрастании аргумента  . На рис. 1 и 2 приведены графики типичных степенных функций с целым положительным показателем:
. На рис. 1 и 2 приведены графики типичных степенных функций с целым положительным показателем:  (кубическая парабола) и
(кубическая парабола) и  (парабола четвертой степени). При
(парабола четвертой степени). При  степенная функция
степенная функция  является линейной функцией, при
является линейной функцией, при  - квадратичной функцией
- квадратичной функцией  .
.
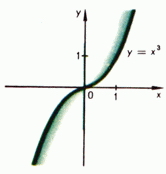
Рис. 1

Рис. 2
Если  - отрицательное целое число
- отрицательное целое число  , то степенная функция определяется равенством
, то степенная функция определяется равенством  . Она определена при всех отличных от нуля
. Она определена при всех отличных от нуля  . Ее график состоит из двух частей (ветвей), имеющих асимптотами оси координат, к которым эти кривые неограниченно приближаются. Типичные представители - функции
. Ее график состоит из двух частей (ветвей), имеющих асимптотами оси координат, к которым эти кривые неограниченно приближаются. Типичные представители - функции  и
и  их графики даны на рис. 3 и 4. При
их графики даны на рис. 3 и 4. При  по определению
по определению  . Если
. Если  , то функция
, то функция  (обозначается также
(обозначается также  ) определяется как обратная функция для функции
) определяется как обратная функция для функции  . При четном
. При четном  функция определена лишь для
функция определена лишь для  , а при нечетном
, а при нечетном  - на всей оси. Графики таких функций
- на всей оси. Графики таких функций  и
и  изображены на рис. 5 и 6.
изображены на рис. 5 и 6.
|
|
|
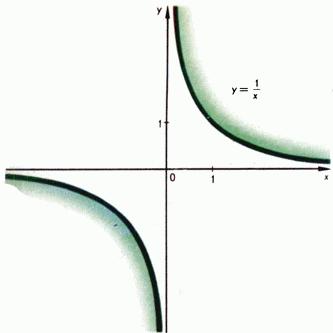
Рис. 3
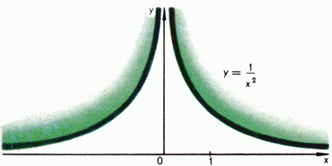
Рис. 4
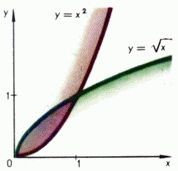
Рис. 5

Рис. 6
Для рационального показателя  (
( - несократимая дробь) степенная функция определяется формулой
- несократимая дробь) степенная функция определяется формулой
 .
.
Графики типичных степенных функций с рациональным показателем приведены на рис. 7, 8, 9.
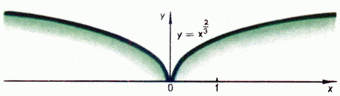
Рис. 7
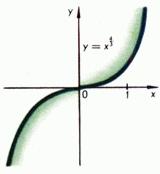
Рис. 8
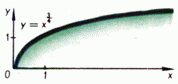
Рис. 9
Степенная функция
Степенная функция – это функция вида y = xn (где x – независимая переменная, n – натуральное число).
Свойства степенной функции различаются в зависимости от того, четным или нечетным является значение n.
 Свойства степенной функции y = xn при четном значении n.
Графиком функции является парабола, расположенная в положительной полуплоскости координат (рис.1).
Свойства степенной функции y = xn при четном значении n.
Графиком функции является парабола, расположенная в положительной полуплоскости координат (рис.1).
Свойства степенной функции y = xn при нечетном значении n. Графиком функции является винтообразная кривая (рис.2).
|
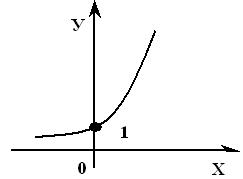
12)Показательная функция,ее общий вид,график и свойства:
Функция вида  называется показательной функцией.
называется показательной функцией.
Замечание. Исключение из числа значений основания a чисел 0; 1 и отрицательных значений a объясняется следующими обстоятельствами:
| a = 0 | Выражения вида 0 x определено при x > 0 и в этом случае тождественно равно нулю. |
| a = 1 | Выражение 1 x определено при всех x, имеет постоянное значение (тождественно единице). |
| a < 0 | Возможно возведение в целую степень или в рациональную степень с нечётным знаменателем. |
Само аналитическое выражение ax в указанных случаях сохраняет смысл и может встречаться в решении задач. Например, для выражения xy точка x = 1; y = 1 входит в область допустимых значений.
Построить графики функций:  и
и  .
.

| 
|

| 
|
| График показательной функции | |
| y = a x, a > 1 | y = a x, 0< a < 1 |
| 
|
|
|
|


