 |
Областью изменения логарифмической функции служит множество всех чисел.
|
|
|
|
3) Все кривые пересекаются с осью х -ов в одной и той же точке, отстоящей от начала координат на + l. Это значит, что при всяком основании логарифм единицы есть нуль (а 0 = 1).
4) Когда a >1, то части кривых, соответствующие абсциссам, меньшим 1, лежат в угле x0 y', а части кривых, соответствующие абсциссам, большим. 1, расположены в угле х0 у. Это значит, что при основании, большем 1, логарифмы чисел, меньших 1, отрицательны, а логарифмы чисел, больших 1, положительны. Это вполне соответствует тому свойству показательной функции, что при положительном значении х функция ах больше 1, а при отрицательном - меньше 1 (если а > 1).
При а< 1 (напр, для кривой y = log1/2 x) заключения противоположны этим.
5) Логарифм самого основания равен 1; так, на графике у = log2 x видно, что абсциссе 2 соответствует ордината 1; на других графиках видно то же самое.
6) При основании, большем 1, ветви кривых, расположенные ниже оси x -ов, при уменьшении абсциссы от 1 до 0, приближаются к полуоси 0 у' как угодно близко, никогда, однако, ее не достигая, а ветви тех же кривых, расположенные выше оси x -ов, при возрастании х от 1 до 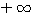 , поднимаются все выше и выше неограниченно.
, поднимаются все выше и выше неограниченно.
Это значит, что (при a >1) с возрастанием числа от 0 до 1 логарифм его возрастает от 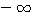 до 0; с возрастанием числа от 1 до
до 0; с возрастанием числа от 1 до 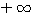 логарифм его возрастает от 1 до
логарифм его возрастает от 1 до 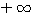 Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1), заключение было бы обратное).
Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1), заключение было бы обратное).
15)Основные типы показательных уравнений их решения:
Показательные уравнения
Уравнения вида af (x) = b, a > 0, a ≠ 1, b > 0
По определению логарифма из основного логарифмического тождества получаем, что 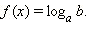 Если f (x) − алгебраическая функция, то и это уравнение будет алгебраическое, которое можно решить с помощью стандартных методов (так как
Если f (x) − алгебраическая функция, то и это уравнение будет алгебраическое, которое можно решить с помощью стандартных методов (так как  − это конкретное число, такое же, как и 5,
− это конкретное число, такое же, как и 5,  π,
π,  и т. п.).
и т. п.).
|
|
|
Уравнения вида 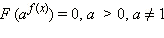
Такие уравнения решаются в два этапа:
a) С помощью замены  это уравнение сводится к уравнению F (t) = 0, у которого ищутся все его положительные корни
это уравнение сводится к уравнению F (t) = 0, у которого ищутся все его положительные корни 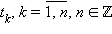 (пусть таких корней ровно n штук).
(пусть таких корней ровно n штук).
b) Для каждого 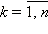 решается уравнение типа рассмотренного выше:
решается уравнение типа рассмотренного выше: 
Эти два типа показательных уравнений являются основными, к ним сводятся все остальные методы.
Пример 1
Решите уравнение

|
Решение
Так как  то, делая замену то, делая замену 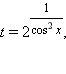 получаем квадратное уравнение получаем квадратное уравнение 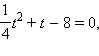 корни которого корни которого 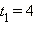 и и  Второй корень, очевидно, посторонний, так как нарушается условие t > 0. Получаем уравнение 1-го типа: Второй корень, очевидно, посторонний, так как нарушается условие t > 0. Получаем уравнение 1-го типа:
Ответ. |
Уравнения вида af (x) = ag (x), a > 0, a ≠ 1
В силу свойств монотонности показательной функции это уравнение равносильно уравнению f (x) = g (x).
Пример 2
Решите уравнение
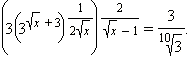
|
Решение
Так как 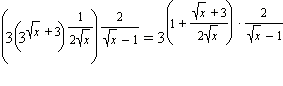 и и 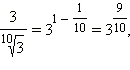 то уравнение можно записать в виде то уравнение можно записать в виде  Следовательно, исходное уравнение равносильно иррациональному уравнению Следовательно, исходное уравнение равносильно иррациональному уравнению  Имеем: Имеем:
Отсюда следует, что Ответ. 25. |
Пример 3
Решите уравнение
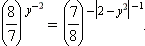
|
Решение
Сразу заметим, что уравнение имеет вид 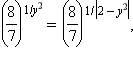 что равносильно уравнению что равносильно уравнению
Ответ. 1, –1. |
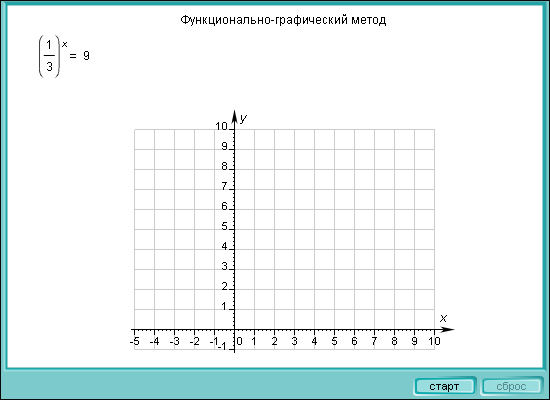
Уравнения вида af (x) = bg (x), a > 0, a ≠ 1, b > 0, b ≠ 1

|
| Модель 3.3. Решение показательных уравнений |
При решении таких уравнений применяется стандартный приём. Прологарифмируем обе его части по любому основанию. В нашем случае удобно логарифмировать по основанию a (или b), то есть по основанию показательной функции, входящей в уравнение:
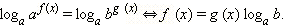
|
А это уравнение уже можно решать стандартными алгебраическими способами, если f (x) и g (x) – алгебраические выражения.
Пример 4
Решите уравнение 
Решение
Уравнение легко преобразовать к виду 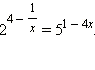 Оно содержит показательные функции с разными основаниями. Для его решения прологарифмируем обе части по любому основанию, например, по основанию 2. Имеем: Оно содержит показательные функции с разными основаниями. Для его решения прологарифмируем обе части по любому основанию, например, по основанию 2. Имеем:
Корни этого уравнения
|
Замечание. Рассмотренный приём перехода от уравнения af (x) = bg (x) к уравнению f (x) = g (x) loga b или, в общем случае, переход от уравнения
| F (x) = G (x) | (1) |
к уравнению
| loga F (x) = logb G (x) (a > 0, a ≠ 0) | (2) |
называется логарифмированием.
Заметим, что переход (1) → (2) в общем случае нарушает равносильность, так как логарифм существует только у неотрицательного числа.
Например, логарифмирование обеих частей уравнения x = x3, которое имеет вид (1), приводит нас к неравносильному уравнению lg x = lg x3 (область определения сузилась). Действительно,
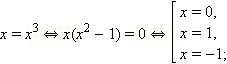
|

|
Таким образом, произошла потеря корней исходного уравнения. Как видно, логарифмирование не является «безобидной» операцией, но в процессе решения уравнения типа af (x) = bg (x) эти неприятности не возникают, так как обе его части положительны.
16)основные типы логарифмических уравнений,их решения:
Логарифмические уравнения
Уравнения вида loga f (x) = b, a > 0, a ≠ 1
Здесь предполагается, что f (x) − функция, уравнения с которой мы уже умеем решать. По определению логарифма из основного логарифмического тождества получаем, что f (x) = ab. Это уравнение можно решать любыми доступными методами, поскольку ab – это число.
Уравнения вида 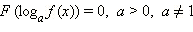
Совершенно аналогично показательным уравнениям, уравнения такого типа решаются в два этапа.
· С помощью замены 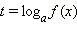 это уравнение сводится к уравнению F (x) = 0, у которого ищутся все его корни
это уравнение сводится к уравнению F (x) = 0, у которого ищутся все его корни 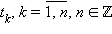 (пусть таких корней ровно n штук).
(пусть таких корней ровно n штук).
· Для каждого 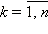 решается уравнение типа рассмотренного выше:
решается уравнение типа рассмотренного выше: 
Понятно, что совершенно не обязательно уравнение будет иметь рассмотренный вид. А значит, в процессе преобразований логарифмических уравнений следует стремиться к тому, чтобы привести все входящие в уравнение логарифмы к одному основанию. При этом необходимо помнить об области определения рассматриваемых выражений, стараясь, чтобы при преобразовании она не уменьшалась, − те корни, которые, возможно, будут приобретены, можно будет отсеять проверкой.
|
|
|
Пример 5
Решите уравнение 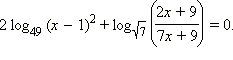
Решение
Преобразуем левую часть уравнения, приводя все логарифмы к основанию 7.
а) б) Поскольку мы использовали, вообще говоря, неравносильное преобразование суммы логарифмов в логарифм произведения (это расширяет область определения), то необходима проверка, которая показывает, что все три найденных числа являются корнями исходного уравнения. Заметим, что число x = 1 рассматривать не нужно, поскольку оно не входит в ОДЗ уравнения. Ответ. 0, 3, −7. |
Пример 6
Решите уравнение

|
Решение
ОДЗ данного уравнения: 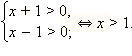 Выполним цепочку преобразований, равносильных в ОДЗ. Выполним цепочку преобразований, равносильных в ОДЗ.
1) 3x – 4 = 0, 2)
x = 0 − не входит в ОДЗ. x = 3 − входит в ОДЗ. Ответ. 3, |
Уравнения вида loga f (x) = loga g (x), a > 0, a ≠ 1


|
| Модель 3.1. Решение логарифмических уравнений |
ОДЗ данного уравнения: 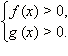 В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:
В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:

|
Полная система равносильности выглядит так:
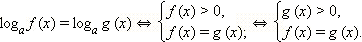
|
Из двух последних систем выбирается та, которая проще (это зависит от конкретного вида функций f (x) и g (x)). На практике, как правило, проще решить уравнение f (x) = g (x) и проверить для его корней положительность одной из функций: f (x) > 0 или g (x) > 0, так как из равенства одной из этих функций следует положительность и другой.
Рассмотренный переход от уравнения loga f (x) = loga g (x) к уравнению f (x) = g (x) называется потенцированием.
Заметим, что потенцирование не является равносильным преобразованием. Область определения уравнения при потенцировании расширяется, так как второе уравнение определено при всех x, для которых определены функции f (x) и g (x), а первое − только при тех x, для которых f (x) > 0 и g (x) > 0.
Пример 7
Решите уравнение 
Решение
Преобразуем сумму логарифмов в логарифм произведения: 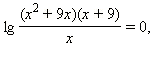 или или 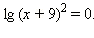 Потенцируя по основанию 10, имеем Потенцируя по основанию 10, имеем  откуда x = –8, x = –10. Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем.
Ответ. x = –10. откуда x = –8, x = –10. Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем.
Ответ. x = –10.
|
|
|
|
17)Иррациональные уравнения и их решения:
|
|
|






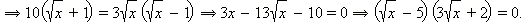
 то есть x = 25; во втором случае
то есть x = 25; во втором случае  − решений нет.
− решений нет.
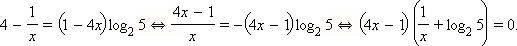
 и
и 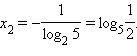 Заметим, что обе части исходного уравнения строго положительны, и поэтому логарифмирование не могло привести ни к потере корней, ни к появлению новых.
Заметим, что обе части исходного уравнения строго положительны, и поэтому логарифмирование не могло привести ни к потере корней, ни к появлению новых.

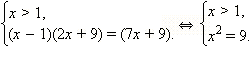 Корень последнего уравнения с учётом ограничения x > 1 есть x = 3.
Корень последнего уравнения с учётом ограничения x > 1 есть x = 3.

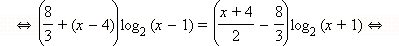
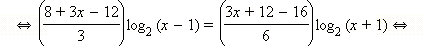


 − входит в ОДЗ.
− входит в ОДЗ. (x + 1 > 0 в ОДЗ),
(x + 1 > 0 в ОДЗ),
