 |
Так как полный оборот вектора приводит его в то же положение, однозначно определить величину угла, если это не оговорено, нельзя.
|
|
|
|
24)определение тригонометрической функции числового аргумента.Область определение тригонометрической функции.:
|
Б) Функция синус


| ||||||||||
Область определения функции— множество Rвсех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная.
Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат.
Функция периодическая с наименьшим положительным периодом 2π:
sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R.
sin x = 0 при x = π·k, k ∈ Z.
sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z.
sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z.
|
Функция косинус


| ||||||||||||||
Область определения функции— множество Rвсех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная.
Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом 2π:
cos(x+2π· k) = cos x, где k ∈ Z для всех х ∈ R.
|
Функция тангенс


| ||||||||||
Множество значений функции — вся числовая прямая, т.е. тангенс — функция неограниченная. Функция нечетная: tg(−x)=−tg x для всех х из области определения. Функция периодическая с наименьшим положительным периодом π, т.е. tg(x+π· k) = tg x, k ∈ Z для всех х из области определения.
|
Функция котангенс


| ||||||||||||
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная. Функция нечетная: ctg(−x)=−ctg x для всех х из области определения.
Функция периодическая с наименьшим положительным периодом π, т.е. ctg(x+π· k)=ctg x, k ∈ Z для всех х из области определения.
|
25)Знаки тригонометрической функции по четвертям:
| Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге. | ||||
| Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге. | ||||
| Функция / четверть | I | II | III | IV |
| sin α | + | + | – | – |
| cos α | + | – | – | + |
| tg α | + | – | + | – |
| ctg α | + | – | + | – |

26)Соотношение между тригонометрическими функциями одного и того же аргумента:
|
27)Формулы приведения:
Формулы приведения
Эти формулы позволяют:
1) найти численные значения тригонометрических функций углов, бо’льших 90°;
2) выполнить преобразования, приводящие к более простым выражениям;
3) избавиться от отрицательных углов и углов, бо’льших 360°.
|
|
|

28)четные и нечетные тригонометрические функции:
|
|
|



 и т. д.
Здесь уже π/4, π/3 и π/6 не углы, выраженные в радианах, а просто числа.
и т. д.
Здесь уже π/4, π/3 и π/6 не углы, выраженные в радианах, а просто числа.






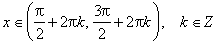



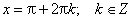






 (1)
(1)
 (2)
(2)

 (5)
(5)
 (6)
(6)
 Аналогично доказывается и тождество (8).
Аналогично доказывается и тождество (8).