 |
Случай уравнения множественной регрессии.
|
|
|
|
Случай уравнения множественной регрессии.
Yt=a0+a1x1t+a2x2t+a3x3t+ut
Сортировка проводится по величине р=|x1|+|x2|+|x3|
Если интерес представляет конкретный регрессор, который приводит к гетероскедастичности, алгоритм повторяется для каждого регрессора в отдельности
В результате обнаруживается регрессор вызывающий гетероскедастичность
Случай уравнения множественной регрессии Имеем:
1. Спецификацию модели:
Yt=a0+a1x1t+a2x2t+a3x3t+ut (10. 5)
2. Выборку наблюдений за переменными {Y, x1, x2, x3}
3. Модель по этим данным гетероскедастична
4. Известны значения σ (ut) в каждом наблюдении
Выводы:
1. Гетероскедастичность приводит к смещенности оценок параметров модели
2. Одним из способов обнаружения гетероскедастичности является тест Голдфелда-Квандта
3. Взвешенный метод наименьших квадратов позволяет получить несмещенные оценки параметров модели в условиях гетероскедастичности
26. Требования, предъявляемые к оценкам параметров моделей,
Оценки параметров модели, полученной по одной и той же выборке(совокупности наблюдений), но методами, использующими различные критерии отбора, будут отличаться как по величине, так и по своим статистическим свойствам. При оценивании параметров регрессионных моделей наиболее часто применяется МНК. Его оценки обладают такими статистическими свойствами, как: несмещенность, состоятельность, эффективность. 1Самое минимальное требование: P (│ b^-b│ > ε )→ 0 при n→ ∞ , где ε –сколько угодно положительное число. Если b^ удовлетвлетворяет этому требованию, то называется состоятельной оценкой величины b. Состоятельность означает стремление приближенного равенства b^ ≈ b кточному равенству по мере увеличения размерности n выборки. В самом деле если св-во состоятельности справедливо, то какое-либо отличие оценки от величины b становится по мере роста объема n выборки невозможным событием. По это причине свойство: P (│ b^-b│ > ε )→ 0 при n→ ∞ представляют в виде P lim b^=b при n→ ∞. Если оценка не обладает этим свойством, то она именуется несостоятельной оценкой. 2Несмещенность E(b^)=b 3. Эффективность оценки
|
|
|
Оценка называется эффективной среди всех оценок параметра, если она имеет минимальную дисперсию среди всех возможных оценок. Последние два свойства противоречат друг другу. Если же этими свойствами оценка обладает лишь в итоге неограниченного увеличения объема n выборки, то оценка называется асимптотически несмещенной и эффективной.
https: //studfile. net/preview/2903223/#: ~: text=%D0%A7%D1%82%D0%BE%D0%B1%D1%8B%20%D0%BF%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D0%BE%20%D0%B8%20%D1%82%D0%BE%D1%87%D0%BD%D0%BE%20%D0%BE%D1%86%D0%B5%D0%BD%D0%B8%D1%82%D1%8C, M%5Bb%5D%3D%EF%81%A2.
27. Понятие адекватности экономических моделей, Проверка статистической гипотезы об адекватности модели,
Под адекватностью понимается возможность получения результата с удовлетворительной точностью. Очевидно, чтобы оценить точность прогноза, необходимо сопоставить вычисленное по модели прогнозное значение эндогенной переменной с ее реальным значением при одинаковых значениях набора регрессоров. Если разница между этими значениями по абсолютной величине окажется приемлемой, то можно будет сделать вывод об адекватном описании поведения объекта полученной моделью. Шаг 1. Имеющаяся выборка делится на две неравные части. Первая объемом 5% - 10% от общего объема выборки, вторая – все остальное. Первую выборку называют контрольной, вторую – обучающей. Из названия понятно, что первая (маленькая) выборка предназначена для тестирования модели на адекватность, вторая (большая) предназначена для оценивания модели. Шаг 2. По обучающей выборке проводится идентификация модели. Шаг. 3. Используя полученные значения оценок параметров модели, вычисляются значения оценок эндогенной переменной для каждой точки контрольной выборки. Шаг 4. Формулируется статистическая гипотеза о равенстве реального и прогнозного значений эндогенной переменной в каждой точке контрольной выборки H0 :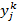 
= 
. Индекс k указывает на принадлежность контрольной выборке, индекс j порядковый номер точки в контрольной выборке. Шаг 5. Вычисляется значение дроби Стьюдента tj= 
и проверяется выполнения условия, что tj= ≤ tкрит. Если условие выполняется в каждой точке контрольной выборки, то делается вывод об адекватности модели с доверительной вероятностью Рдов.
|
|
|
Если случайные остатки в уравнениях наблюдений Yt=a0+a1x1t+a2x2t+a3x3t+ut некоррелированы, но гетероскедастичны, то оптимальная линейная процедура оценивания параметров модели именуется взвешенным методом наименьших квадратов, разработанным Гауссом. В этом частном случае матрица Cov( 
, 
) является диагональной, но не скалярной. 
, где Р матрица ковариаций случайных возмущений в уравнения наблюдений. Теорема. Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является: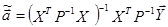 
.
В общем случае, когда не выполняются предпосылки теоремы гаусса-Маркова 2 и 3, тогда: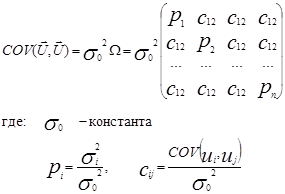 
Теорема Эйткена, которая формулирует наилучшую линейную процедуру оценки параметров линейной модели множественной регрессии в подобном случае: В классе линейных несмещенных оценок вектора параметров линейной модели множественной регрессии, 
T, наилучшей является оценка: 
. Процедура называется обобщенным методом наименьших квадратов. От классического метода наименьших квадратов он отличается тем, что оценки параметров находятся из условия минимальности функционала: Q= 
Ω -1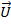 
. Если: Ω =E, то выражение превращается в МНК, если pi≠ Const, а Cij=0 –превращается в ВМНК. В заключении отметим, что применение ОМНК требует знания ковариационной матрицы вектора случайных возмущений Ω, что встречается крайне редко. На практике используется, так называемый, доступный обобщенный метод наименьших квадратов. К нему относят те процедуры ВМНК и процедуры устранения автокорреляции.
|
|
|
|
|
|
