28. Линейная модель парной регрессии, Оценка параметров модели с помощью метода наименьших квадратов (МНК), 

28. Линейная модель парной регрессии, Оценка параметров модели с помощью метода наименьших квадратов (МНК),       

http: //sun. tsu. ru/mminfo/2016/Dombrovski/book/chapter-2/chapter-2. htm

Как было отмечено в предыдущей главе, одной из типичных задач, которую часто приходится решать на практике, является установление и количественная оценка связи и влияния нескольких (или одной) независимых переменных на зависимую переменную. Для решения подобного рода проблем в эконометрике используются методы регрессионного анализа.

В наиболее общей постановке задача заключается в следующем. Объект исследования представлен наблюдаемыми величинами y, x₁, x₂,..., x_k. Предполагается, что между этими величинами существует объективная причинная связь, то есть на основе предварительного анализа объекта установлено, что наблюдаемая величина y зависит от наблюдаемых величин x₁, x₂,..., x_k. Эту связь между зависимой переменной y и независимыми переменными x₁, x₂,..., x_k в принципе можно представить в виде функциональной, в общем случае нелинейной, зависимости, определенной с точностью до параметров, то есть связь между переменными в регрессионных моделях в общем случае определяется выражением

,

(2. 1)

где 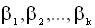- параметры (коэффициенты) регрессионной модели. В данное уравнение включена зависимость от переменной u, которая отражает тот факт, что в действительности на практике наблюдаемые величины отклоняются от этой функциональной зависимости. В регрессионном анализе предполагается, что эти отклонения носят случайный характер и поэтому моделируются с помощью введения в функциональную зависимость случайной переменной u. Более подробно характер и природа этой переменной будут рассмотрены ниже. Заметим только, что от правильности предположений относительно случайной составляющей модели и проверки выполнения их на практике в решающей степени зависит успех всего эконометрического моделирования.

Функциональная зависимость вида ( 2. 1 ) называется регрессионной, а уравнение ( 2. 1 ) - регрессионным.

Замечание относительно терминологии.

В регрессионном анализе зависимую (объясняемую) переменную называют регрессанд, а независимые переменные - регрессорами. В эконометрике часто для этих переменных используют также термины эндогенная и экзогенные переменные.

В зависимости от количества регрессоров регрессионные модели подразделяются на модели парной регрессии (одна независимая переменная) и модели множественной или многомерной регрессии (несколько независимых переменных).

В зависимости от вида функциональной связи регрессионные модели делятся на линейные и нелинейные.

В данном разделе рассматривается метод оценки параметров парной линейной регрессии, называемый методом наименьших квадратов (МНК). Метод наименьших квадратов имеет важнейшее значение во многих областях науки и техники, и применяется, как только возникает необходимость оценивания некоторых величин на основе статистической информации (эмпирических данных). Многие статистические процедуры оценки параметров как линейных, так и нелинейных моделей основаны на методе наименьших квадратов. Не преувеличивая можно сказать, что такие величайшие достижения, как запуск человека в Космос или посадка на Луну, стали возможны благодаря методу наименьших квадратов.

Этот метод и многочисленные его модификации являются основными и в эконометрике. Поэтому при изучении данного курса ему нужно уделить особое внимание.

2. 2. 1. Критерий наименьших квадратов. Сравнение с другими возможными критериями

Запишем уравнение для отдельных наблюдений (реализаций) в парной линейной регрессии

(2. 5)

где t=1, 2, …, n. Уравнение ( 2. 5 ) выражает теоретическую связь между зависимой y и независимой x переменными в конкретных наблюдениях (см. рис. 2. 1 ). В это уравнение входят теоретические значения параметров 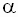, 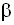и реализации случайной составляющей u, которые определяют объективную связь между переменными, но неизвестны исследователю и могут быть лишь приближенно оценены на основе имеющихся наблюдений. 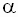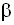Обозначим оценки параметров и соответственно символами a и b. Эти оценки называются эмпирическими, поскольку их можно определить только на основе эмпирических данных. Если они каким-либо образом определены, то можно записать

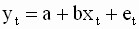
(2. 6)

где e_t - ошибки модели (другой, часто используемый в эконометрике термин - остатки модели). Очевидно, что

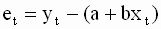
Уравнение ( 2. 6 ) выражает эмпирическую взаимосвязь между переменными модели и его можно записать только относительно конкретных наблюдений. Подчеркнем, что ошибки модели являются наблюдаемыми величинами, поскольку их можно определить исходя из наблюдений переменных модели.

В методе наименьших квадратов оценки a и b параметров модели строятся так, что бы минимизировать сумму квадратов ошибок (остатков) модели по всем наблюдениям. Таким образом, критерий (целевая функция) наименьших квадратов записывается в виде

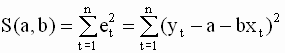
(2. 7)

Очевидно, правая часть выражения ( 2. 7 ) является квадратичной функцией параметров a и b.

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: