Замечание относительно переменных x.

Замечание относительно переменных x.

Отметим, что на этапе формулирования критерия наименьших квадратов нам не понадобились какие-либо дополнительные (ограничивающие) предположения относительно характера независимых переменных x модели - случайные они или детерминированные. При выводе уравнений для оценок эти предположения не имеют значения.

Прежде чем переходить к формальному выводу уравнений для оценок, проиллюстрируем принцип метода наименьших квадратов графически. На рис 2. 2. стороны квадратов равны ошибкам модели в каждом из наблюдений. Параметр a характеризует сдвиг линии относительно начала координат, параметр b - наклон этой линии относительно оси x. В методе наименьших квадратов оценки a и b истинных значений параметров выбираются так, чтобы сумма площадей квадратов была минимальна.

Графическая иллюстрация принципа наименьших квадратов

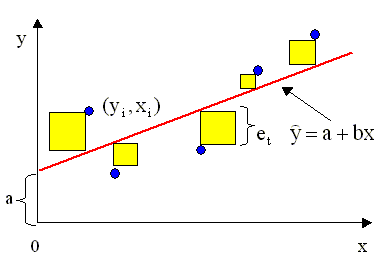
Рис 2. 2. Иллюстрация принципа наименьших квадратов

Замечание относительно выбора критерия - почему не другие критерии?

Существует множество других критериев, которые в принципе можно использовать при построении эмпирических оценок параметров модели. Однако некоторые из них приводят к неоднозначным результатам и, несмотря на наглядность, не пригодны для использования. Например, почему бы не попытаться минимизировать просто сумму ошибок (остатков) модели, а не их квадратов. Очевидно, такой подход приводит к неоднозначному решению - можно бесконечным множеством способов провести прямую линию в плоскости (y, x) так, чтобы сумма остатков была равна нулю. При этом, как показано на рис. 2. 3., между переменными y и x может вообще не существовать никакой зависимости.

Рис 2. 3. Между переменными нет зависимости

Другой, более приемлемый критерий - минимизировать сумму абсолютных величин остатков. Формально вывести выражения для оценок параметров с использованием этого критерия возможно, однако статистические свойства этих оценок и модели в целом установить сложно, поэтому данный критерий не получил широкого распространения.

Существуют статистические критерии, такие, например, как критерий максимума правдоподобия (МП). Эти критерии требуют знания или определенных предположений относительно вида вероятностного распределения случайных составляющих модели. Подробный сравнительный анализ МНК и МП методов будет проведен в последующих разделах.

2. 2. 2. Вывод нормальных уравнений для оценок параметров регрессии. Решение нормальных уравнений. Варианты записи выражений для оценок параметров

Получим выражения для оптимальных в смысле минимума МНК-критерия оценок параметров модели парной линейной регрессии.

Согласно методу наименьших квадратов, необходимо минимизировать функцию двух переменных

(2. 8)

по всем возможным значениям a и b при заданных (наблюдаемых) значениях x₁,..., x_n, y₁,..., y_n.

Из курса высшей математики известно, что условием минимума функции вида ( 2. 8 ) по переменным a и b является равенство нулю частных производных этой функции. Уравнения для определения оптимальных оценок получаются путем приравнивания нулю производной функции S(a, b) как функции только от a при фиксированном b и производной функции S(a, b ) как функции только от b при фиксированном a.

Это приводит к следующей системе уравнений:

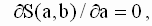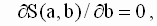
которую необходимо решить относительно переменных a и b. По правилам вычисления производных получим следующие выражения:

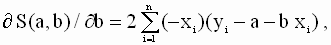
так что значения параметров a и b, минимизирующие квадратичную форму ( 2. 8 ), удовлетворяют соотношениям

	(2. 9)
	(2. 10)

После несложных преобразований эту систему можно записать в виде

	(2. 11)
	(2. 12)

Система уравнений ( 2. 11 ), ( 2. 12 ) называется системой нормальных уравнений для коэффициентов регрессии.

Это система двух линейных уравнений с двумя неизвестными и она легко может быть решена, например, методом подстановки.

Из первого уравнения системы находим:

где , - выборочные средние наблюдений.

Подставив выражение для a во второе уравнение системы, получим

,

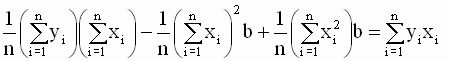откуда

,

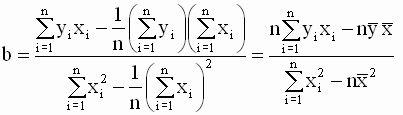Таким образом, мы получили следующие соотношения для оценок параметров модели

,

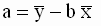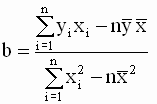
Однако, в теоретических исследованиях и практических расчетах чаще используют другую, более удобную эквивалентную форму записи уравнений для оценок. Эта форма получается, если использовать следующие соотношения

Эти соотношения позволяют получить новую форму записи выражения для b (в отклонениях от выборочных средних значений)

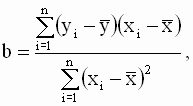
(2. 13)

которая вместе с выражением для a

(2. 14)

дает решение задачи определения оптимальных оценок. Полученные оценки (независимо от формы записи) называют оценками наименьших квадратов. Заметим, что решение может существовать только при выполнении условия

(2. 15)

которое означает, что определитель системы нормальных уравнений отличен от нуля. Действительно, этот определитель равен

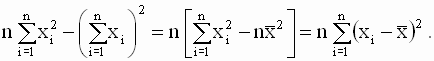
Условие ( 2. 15 ) называется условием идентифицируемости модели наблюдений , и означает, что не все значения x₁,..., x_n совпадают между собой. При нарушении этого условия все точки (x_i, y_i), i = 1,..., n, лежат на одной вертикальной прямой . В модели парной линейной регрессии это условие практически всегда выполняется, чего нельзя сказать о многомерной регрессии. Его не выполнение в многомерном случае приводит к так называемой проблеме мультиколлинеарности, которая подробно будет рассмотрена в главе, посвященной многомерной регрессии.

Выражение для коэффициента b часто записывают также, используя понятия выборочной вариации (дисперсии) и выборочной ковариации.

Выборочная вариация определяется соотношением вида

(2. 16)

и выборочная ковариация следующим соотношением

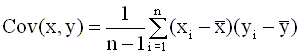
(2. 17)

Используя введенные понятия, формулу ( 2. 13 ) для коэффициента b можно записать в виде

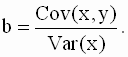
(2. 18)

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: