Пример 2.2. Задание.. 29. Построение нелинейных экономических моделей

Пример 2. 2.

Торговое предприятие имеет несколько филиалов. Исследуем зависимость годового товарооборота отдельного филиала от: а) размера торговой площади; б) среднедневной интенсивности потока покупателей. Поскольку мы пока не умеем строить модели множественной регрессии, построим две " частные" модели парной регрессии.

Таким образом, объясняемая переменная y - годовой товарооборот филиала (млн. руб. ), объясняющая переменная в первой модели - размер торговой площади (тыс. кв. м. ), обозначим ее x₂, во второй модели - интенсивность потока покупателей (тыс. чел. в день), обозначим ее x₃. Исходные данные для двенадцати филиалов приведены в таблице 1. 2. (источник: Й. Грубер, 1996, [ 12 ]).

Таблица 1. 2

На рис. 2. 5а, 2. 5б приведены диаграммы рассеяния для пар переменных (y, x₂) и (y, x₃). Оцененные значения коэффициентов первой регрессии: a=0, 6057, b=5, 2221. Ее уравнение имеет вид

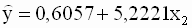
Для второй регрессии получаем следующие оценки: a=-2, 0394, b=0, 6846. Ее уравнение

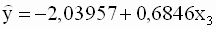
На рис. 2. 5а, 2. 5б приведены оцененные значения зависимой переменной (изображены в виде квадратов) в обеих регрессиях. Из этих рисунков видно, что переменная x₂ (" торговая площадь" ) лучше объясняет поведение переменной y (" товарооборот" ), чем переменная x₃ (" среднедневная интенсивность покупателей" ). Однако визуальное сравнение различных регрессий далеко не всегда позволяет оценить качество модели и выявить наилучшую из них. Поэтому в последующих разделах будут рассмотрены объективные критерии качества регрессионных моделей.

Задание.

Дайте интерпретацию параметров регрессий примера 2. 2.

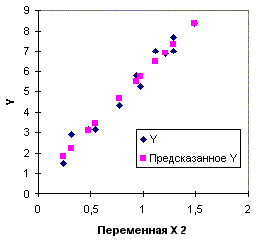
Рис. 2. 5а. Диаграмма рассеяния и линия
регрессии (первая модель, пример 2. 2)

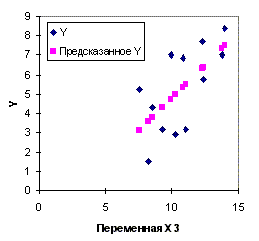
Рис. 2. 5б. Диаграмма рассеяния и линия
регрессии (вторая модель, пример 2. 2)

29. Построение нелинейных экономических моделей   

Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование возможно лишь на основе нелинейных уравнений регрессии. Различают два вида нелинейных моделей: нелинейные модели по переменным и нелинейные модели по параметрам. Основные типы нелинейных моделей: 1) Обобщенная модель нелинейная по переменным 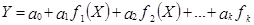, 2)Степенные функции , 3) Показательные функции ., 4) Показательно-степенные функции Y_t =a₀ (1+u_t). Основной прием, который используется для построения нелинейных регрессионных моделей – линеаризация, который заключается в искусственном преобразовании исходной спецификации модели к линейному виду. Линеаризация обобщенной нелинейной модели: 1. Вводятся новые переменные: 2. Подставляя новые переменные в модель (1), получим модель линейную по переменным z: 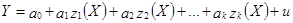. Линеаризация степенной модели, нелинейной по параметрам: 1. Метод линеаризации – логарифмирование с последующим введением новых переменных: 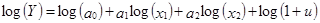2. Вводятся новые переменные и параметры: 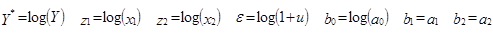. В новых переменных исходное уравнение принимает вид уравнения множественной регрессии . 3. Оцениваются параметры b₀, b₁, b₂ – методом наименьших квадратов и проверяются гипотезы о выполнении предпосылок теоремы Гаусса-Маркова для модели. 4. Осуществляется возврат к исходной модели 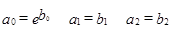. Линеаризация показательной (экспоненциальной) модели: 1. Метод линеаризации – логарифмирование 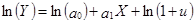. 2. Введение новых переменных и параметров: . 3. Оценка линейной регрессионной модели 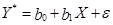. 4. Обратный переход к исходной модели. Линеаризация показательно-степенной модели: производится так же с помощью логарифмирования и последующей замены переменных.