 |
Замечание относительно выборочных дисперсии и ковариации.
|
|
|
|
Замечание относительно выборочных дисперсии и ковариации.
Напомним, что выборочная дисперсия характеризует степень разброса случайной величины относительно ее выборочного среднего значения. Выборочная ковариация характеризует степень линейной статистической взаимосвязи двух случайных величин. При определенных условиях, которые будут рассмотрены позже, выражения ( 2. 16 ) и ( 2. 17 ) являются несмещенными эмпирическими оценками теоретических дисперсии и ковариации.
Иногда выборочные дисперсию и ковариацию определяют делением не на (n - 1), а на n. Такие оценки этих величин являются смещенными.
Из выражения ( 2. 18 ) видно, что значения b будут тем меньше, чем меньше ковариация между наблюдаемыми значениями переменных x и y и чем больше значения выборочной дисперсии Var(x). Кроме того, знак b совпадает со знаком ковариации Cov(x, y), поскольку Var(x)> 0.
Замечание относительно полученных оценок.
Оценки вида ( 2. 13 ), ( 2. 14 ) (или в других формах записи) являются выборочными эмпирическими оценками истинных (теоретических) параметров линейной регрессии. Эти оценки являются линейными относительно наблюдений. Эти оценки являются случайными величинами, поскольку зависят от случайных наблюдений.
Если независимая переменная не случайная (детерминированная) величина, то ее дисперсия равна нулю, а ковариация детерминированной и случайной величин равна нулю. В этом случае выборочные дисперсия (вариация) x и выборочная ковариация величин x и y теряют смысл оценок соответствующих теоретических значений дисперсии и ковариации и должны рассматриваться только как некоторые характеристики наблюдаемых переменных, не связанные с их статистическими свойствами.
|
|
|
И, наконец, подчеркнем еще раз, что уравнения для оценок получены без каких либо предположений относительно характеристик случайных составляющих модели.
Интерпретация оценок параметров
Определим оценку 
зависимой переменной y уравнением
| (2. 19) |
Уравнение ( 2. 19 ) определяет эмпирическую регрессионную функцию, оценка называется прогнозом объясняемой переменной. Эта функция определяет прямую на плоскости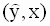 
. Эмпирический коэффициент b является частной производной ( 2. 19 ) по независимой переменной x (регрессору). Следовательно можно дать следующую интерпретацию коэффициента b: изменение величины независимой переменной x на единицу при фиксированном значении параметра a приведет к изменению оценки переменной y на величину коэффициента b.
Пример 2. 1.
Одним из ключевых понятий фондового рынка является понятие компании - лидера, изменение курса акций которой влияет на движение курсов акций других компаний данного сектора или отрасли экономики. Такое влияние может быть обусловлено технологической взаимосвязанностью компаний, однородностью выпускаемой продукции, монополизацией рынка и прочими причинами. Для количественного анализа влияния доходностей акций компании - лидера на доходности акций других компаний применяются методы регрессионного анализа. В таблице 1. 1. приведены данные по годовым доходностям акций двух компаний А и Б, относящихся к одной отрасли (числовые данные из кн. Л. О. Бабешко, 2001. [ 4 ]). Построим модель парной регрессии для изучения зависимости доходности акций компании А от доходности акций компании Б.
Таблица 1. 1
Из диаграммы рассеяния, построенной по этим данным (рис. 2. 4a ), можно предположить существование линейной зависимости между переменными y и x.
Рис. 2. 4а. Диаграмма рассеяния примера 2. 1
Рис. 2. 4б. Линия регрессии (пример 2. 1)
|
|
|
Оценки параметров парной линейной регрессии, вычисленные по формулам ( 2. 13 ), ( 2. 14 ) равны: a=4, 02; b=1, 29. Уравнение регрессии имеет вид
|
Оцененные значения зависимой переменной приведены на рис. 2. 4б. Параметрам модели можно дать следующую интерпретацию. При x = 0 (доходность акций компании B равна нулю), ожидаемая (прогнозируемая) доходность акций компании A равна 4, 02%. При увеличении доходности акций компании B на 1%, прогнозируемая доходность акций компании A вырастет на 1, 29%. Таким образом, акции данной компании можно рассматривать как " агрессивные" по отношению к акциям компании B - оцененный коэффициент " бета" для них больше единицы.
|
|
|
