 |
32. Ошибки спецификации моделей, их последствия и способы устранения,
|
|
|
|
32. Ошибки спецификации моделей, их последствия и способы устранения,
Возможные ошибки спецификации модели:
1. Неправильный выбор вида уравнения регрессии
2. В уравнение регрессии включена лишняя (незначимая) переменная
3. В уравнении регрессии пропущена значимая переменная
- Неправильный выбор вида функции в уравнении
Пусть на первом этапе была сделана спецификация модели в виде:
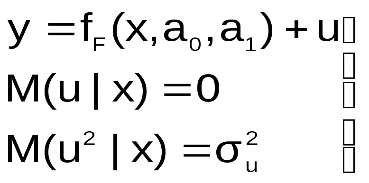
в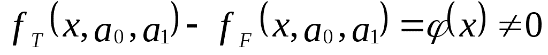 
которой функция fF(x, a0, a1) выбрана не верно. Предположим, что yT=fT(x, a0, a1)+v – правильный вид функции регрессии. Тогда справедливо выражение:
И 
з выражения следует:
Иными словами, математические ожидания эндогенной переменной, полученные с помощью функций fT и fF не совпадают, т. е. первая предпосылка теоремы Гаусса-Маркова M(ulx)=0 не выполняется
Следовательно, в результате оценивания такой модели параметры а0 и а1 будут смещенными
Симптомы наличия ошибки спецификации первого типа:
1. Несоответствие диаграммы рассеяния, построенной по имеющейся выборке виду функции, принятой в спецификации
2. В динамических моделях длительно сохраняется знак значений оценок случайных возмущений у смежных (по номеру t ) уравнений наблюдений
Именно этот симптом и улавливается статистикой DW Дарбина–Уотсона!
В силу данного обстоятельства тесту Дарбина–Уотсона в эконометрике придается большое значение.
Способ устранения: выбор другой формы спецификации модели. Например, нелинейная вместо линейной и т. д.
2. В уравнение регрессии включена лишняя переменная
П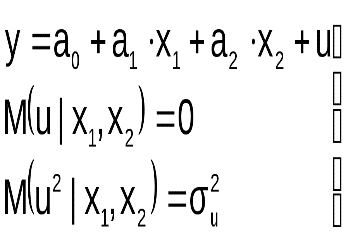 
усть на этапе спецификации в модель включена «лишняя» переменная, например, X2
« 
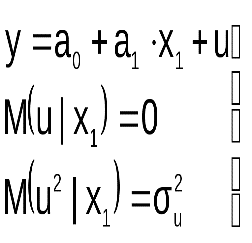Правильная» спецификация должна иметь вид:
Последствия:
1. Оценки параметров а0, а1, а2 останутся несмещенными, но потеряют свою эффективность (точность)
|
|
|
2. Увеличивается ошибка прогноза по модели
как за счет ошибок оценок коэффициентов и σ u, так и за счет последнего слагаемого. Это особенно опасно при больших абсолютных значениях регрессора
Диагностика:
В моделях множественной регрессии необходимо для каждого коэффициента уравнения проверять статистическую гипотезу H0: ai=0. Вспомним, что для этого достаточно оценить дробь Стьюдента и сравнить ее значение с критическим значением распределения Стьюдента, которое вычисляется по значению доверительной вероятности и значению степени свободы n2 = n – (k+1)
3 
. В модели не достает важной переменной
Последствия такие же, как и в первом случае: получаем смещенные оценки параметров модели
Для устранения необходимо вернуться к изучению особенностей поведения экономического объекта, выявить опущенные переменные и дополнить ими модель
33. Показатели качества спецификации линейной модели
Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным.
Для оценки качества модели регрессии используются специальные показатели.
Качество линейной модели парной регрессии характеризуется с помощью следующих показателей:
1) парной линейный коэффициент корреляции, который рассчитывается по формуле:
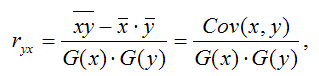
где G(x) – среднеквадратическое отклонение независимой переменной;
G(y) – среднеквадратическое отклонение зависимой переменной.
Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии
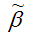
по формуле:
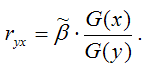
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах [-1; +1]. Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.
|
|
|
2) коэффициент детерминации рассчитывается как вадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.
Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий.
Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии:
G2(y)=? 2(y)+? 2(y),
где G2(y) – это общая дисперсия зависимой переменной;
? 2(y) – это объяснённая с помощью построенной модели регрессии дисперсия переменной у, которая рассчитывается по формуле:
? 2(y) – необъяснённая или остаточная дисперсия переменной у, которая рассчитывается по формуле:
С использованием теоремы о разложении дисперсий рассчитываются следующие показатели качества линейной модели множественной регрессии:
1) множественный коэффициент корреляции между зависимой переменной у и несколькими независимыми переменными хi:
Данный коэффициент характеризует степень тесноты связи между зависимой и независимыми переменными. Свойства множественного коэффициента корреляции аналогичны свойствам линейнойго парного коэффициента корреляции.
2) теоретический коэффициент детерминации рассчитывается как квадрат множественного коэффициента корреляции:
|
|
|
Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимых переменных;
3) показатель
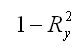
характеризует в процентном отношении ту долю вариации зависимой переменной, которая не учитывается а построенной модели регрессии;
4) среднеквадратическая ошибка модели регрессии (Mean square error – MSE):
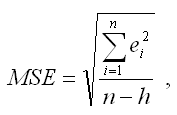
где h– это количество параметров, входящих в модель регрессии.
Если показатель среднеквадратической ошибки окажется меньше показателя среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений ? (у), то модель регрессии можно считать качественной.
Показатель среднеквадратического отклонения наблюдаемых значений зависимой переменной от модельных значений рассчитывается по формуле:
5) показатель средней ошибки аппроксимации рассчитывается по формуле:
Если величина данного показателя составляет менее 6-7%, то качество построенной модели регрессии считается хорошим. Максимально допустимым значением показателя средней ошибки аппроксимации считается 12-15 %.
|
|
|
