 |
Учебное пособие. Методические указания по решению задач в рабочей тетради. Содержание. Модуль №1. Задача №1. Федеральное агентство по образованию
|
|
|
|
Федеральное агентство по образованию
Тольяттинский государственный университет
Кафедра «Начертательная геометрия и черчение»
УЧЕБНОЕ ПОСОБИЕ
по курсу «Начертательная геометрия»
Методические указания по решению задач в рабочей тетради
Тольятти 2007
Содержание
Модуль №1. 4
Точка. 4
Задача №1. 4
Задача №2. 7
Линия. 9
Задача №3. 9
Задача №4. 9
Задача №6. 10
Задача №8. 11
Задача №10. 12
Задача №11. 13
Задача №13. 14
Задача №12. 16
Модуль №2. 19
Плоскость. 19
Задача №17. 19
Задача №18. 21
Задача №20. 24
Задача №21. 26
Задача №22. 26
Задача №23. 28
Задача №24. 31
Задача №25. 31
Задача №26. 34
Задача №27. 36
Задача №30. 37
Задача №31. 37
Поверхность. 41
Задача №32. 41
Задача №23. 42
Задача №34. 44
Задача № 35. 47
Задача №36. 50
Задача №37. 50
Задача №38. 53
Задача №40. 57
Задача №41. 57
Задача №42. 60
Задача №43. 63
Задача №46. 65
Задача №47. 69
Задача №47. 72
Задача №48. 73
Задача №50. 75
Модуль №3. 79
Главные позиционные задачи. 79
Решение задач по 1 и 2 алгоритмам.. 79
Задача №55. 79
Задача №57. 80
Задача №58. 81
Задача №60. 84
Задача №61. 92
Задача №64. 94
Задача №67. 96
Задача №71. 99
Задача №73. 103
Задача №76. 106
Задача №78. 108
Модуль №4. 110
Метрические задачи. 110
Задача №81. 110
Задача №82. 111
Задача №83. 112
Задача №84. 113
Задача №85. 113
Задача №86. 114
Задача №87. 115
Задача №88. 116
Задача №89. 116
Задача №90. 118
Задача №91. 119
Задача №92. 120
Задача №93. 121
Задача №95. 122
Метод введения новой плоскости проекций. 123
Задача №100. 123
Задача №101. 126
Задача №102. 127
Задача №103. 130
Задача №104. 130
Задача №105. 132
Задача №106. 134
Задача №107. 136
Задача №107. 138
Задача №109. 141
Задача №110. 145
Метод вращения вокруг проецирующей оси. 148
Задача №115. 148
|
|
|
Задача №116. 149
Задача №117. 150
Модуль №1
Точка
Задача №1
Построить комплексные чертежи точек: А(15, 30, 0), В(30, 25, 15), С(30, 10, 15), D(15, 30, 20)
Решение задачи разделим на четыре этапа.
1. А(15, 30, 0); xA= 15 мм; yA = 30мм; zA = 0.
Как Вы думаете, если у точки А координата zA=0, то какое положение она занимает в пространстве?

Рис. 1. 1
Так выглядит комплексный чертеж точки А построенный по заданным координатам
Если у точки одна координата равна нулю, то точка принадлежит одной из плоскостей проекции. В данном случае у точки нет высоты: z = 0, следовательно точка А лежит в плоскости П1.
На комплексном чертеже оригинал (т. е. сама точка А) не изображается, есть только ее проекции.
2. В(30, 25, 15) и С(30, 10, 15).
На втором этапе объединим построение двух точек.
xB = 30мм; xC = 30мм
yB = 35мм; yC = 10мм
zB = 15мм; zC = 15мм
У точек В и С: xB = xC = 30мм, zB = zC = 15мм
а) Координаты х точек одинаковы, следовательно, в системе П1 – П2 проекции точек лежат на одной линии связи (рис. 1. 2),
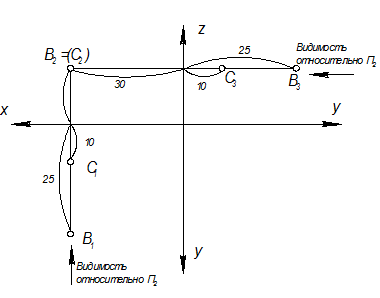
Рис. 1. 2
б) Координаты z точек совпадают, (обе точки одинаково удалены от П1 на 15мм, ) т. е. они расположены на одной высоте, следовательно на П2 проекции точек совпадают: В2 = (С2).
в) Для определения видимости относительно П2 смотрим на рис. 1. 3. Наблюдатель видит точку В, которая закрывает собой точку С, т. е. точка В расположена ближе к наблюдателю, поэтому на П2 она видима. (См. М1 - 13 и 16).

Рис. 1. 3
В системе П2П3 проекции точек также лежат на одной линии связи и видимость определяется по стрелке (рис. 1. 2).
Точки В и С - называются фронтально конкурирующими.
3. D(15, 30, 20); xD = 15мм; yD = 30мм; zD = 20мм.
а) На этом комплексном чертеже (рис. 1. 4) построены три проекции точки D(D1, D2, D3).
Все три координаты имеют числовые значения, отличные от нуля, поэтому точка не принадлежит ни одной плоскости проекций.

Рис. 1. 4
б) Совместим пространственное изображение А и D (рис. 1. 5). В системе П1-П2 проекции точек А и D лежат на одной линии связи, только точка D выше точки А, следовательно D - видима, а А - невидима (видима на П1 та точка, которая расположена выше)
|
|
|

Рис. 1. 5
На четвертом, завершающем этапе, соединим все три фрагмента комплексных чертежей точек А, В, С, D в один общий.
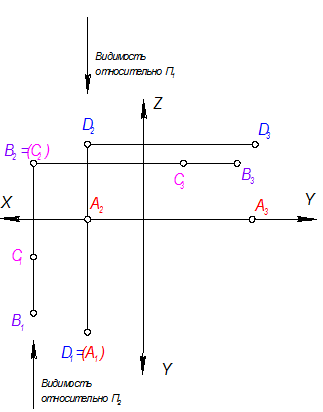
Рис. 1. 6
Точки А и D - называются горизонтально конкурирующими.

Рис. 1. 7
Задача №2
На заданных линиях связи построить проекции точек В и С: точка В расположена выше точки А на 10мм и ближе к наблюдателю на 15мм; точка С расположена ниже точки А на 10мм и ближе к плоскости П2 на 5мм.
Решение задачи осуществляется на безосном комплексном чертеже.
1. Распределим линии связи для точек В и С

2. Проведем вспомогательные линии ^ А1А2, пересекая линии связи точек В и С.
Верхняя горизонтальная линии от А2 будет определять уровень точек В и С относительно П1, по сравнению с точкой А, т. е. " выше - ниже" А:
Точка В выше на 10мм, чем точка А относительно П1
Точка С ниже на 10мм, чем точка А относительно П1
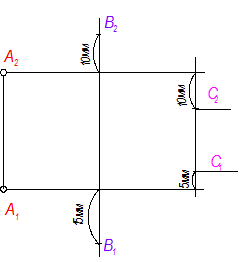
3. Нижняя горизонтальная линия от А1 будет границей расположения точек В и С относительно П2, по сравнению с точкой А, т. е. " ближе - дальше" от наблюдателя:
Точка В ближе на 15мм к наблюдателю, чем А,
Точка С дальше от наблюдателя, т. е. ближе к П2 на 5мм, чем точка А.
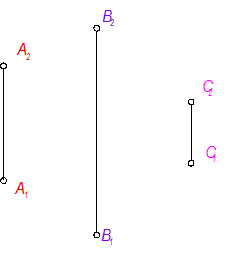
4. Убираем все вспомогательные построения.
|
|
|


