 |
Задача решена. Построить проекции отрезка АВ горизонтали h(h1h2) || П1 если Ðb=30°, |АВ| = 40мм, точка В удалена от П2 дальше, чем точка А
|
|
|
|
Задача решена.
Линия
Задача №3
Для решения этой задачи, при необходимости, можно воспользоваться Модулем №1(стр. 20)
Задача №4
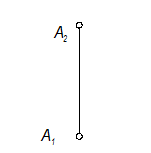
Построить проекции отрезка АВ горизонтали h(h1h2) || П1 если Ð b=30°, |АВ| = 40мм, точка В удалена от П2 дальше, чем точка А.
Решить эту задачу, значит построить точка В(В1В2).
h2 ^ линии связи,
h1 - проецируется в истинную величину;
Ð b - угол наклона горизонтали к П2 проецируется без искажения.
Алгоритм построения.
1. Горизонталь начинаем строить с фронтальной плоскости: h2 ^ лин. связи. Можно ли отложить на этой линии 40мм и построить точку В2? Нельзя, т. к. h2 проецируется с искажением.

2. На П1 проведем вспомогательную прямую из А ^ А1А2.
3. Построим угол Ð b. Его можно отложить вверх от вспомогательной линии и вниз, но в задаче дано, что точка В удалена от П2 дальше, чем точка А, поэтому луч для Ð b = 30° откладываем вниз.
4. На этом луче откладываем расстояние, равное 40мм и получаем: h1 = А1В1 = |АВ|
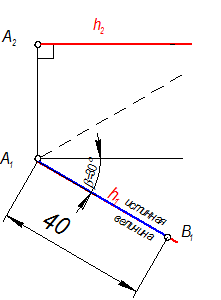
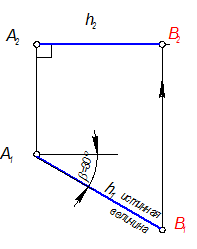
5. Так как мы построили горизонтальную проекцию точки В Þ В1, то для определения В2 достаточно провести линию связи до пересечения с h2 Þ В2.
Задача №6
Построить проекции отрезка |МN| =30мм горизонтально проецирующей прямой при условии, что точка В делит отрезок пополам.

1. Горизонтально проецирующая прямая MN параллельна сразу двум плоскостям проекций: П1 и П2.

Отложить 15мм вверх и вниз от точки В2
2. Фронтальная ее проекция – M2N2 проецируется без искажения на П2 и совпадает с линиями связи, а горизонтальная проекция проецируется в точку, которая называется главной проекцией и обладает собирательными свойствами (М1=N1=В1).

B1=N1=M1 – горизонтально конкурирующие точки
|
|
|
Задача №8
Определить истинную длину отрезка АВ и углы его наклона к плоскостям проекций П1 и П2
1. Анализ условия: ни одна из проекций отрезка АВ не || и не ^ линиям связи, значит задана прямая общего положения (Модуль №1, стр. 20).

A1B1 – первый катет. Перпендикуляр к A1B1 можно провести как из точки A1 так и из В1
2. Двухкартинный чертеж Монжа обратим, поэтому для нахождения натуральной величины отрезка АВ применяют метод прямоугольного треугольника. (Модуль №1, стр. 14).

А1А0 – второй катет. Гипотенуза А0В1 – это натуральная величина |AB| - это натуральная величина |AB|. Угол a - есть угол наклона AB к П1.
Аналогично, можно найти натуральную величину отрезка АВ и угол (b) наклона данного отрезка АВ к П2, построив прямоугольный треугольник на П2. Самостоятельно.
Задача №10
Построить горизонтальную проекцию отрезка АВ, если Ð b = 20° (угол наклона к П2), точка В дальше от П2, чем точка А.
Решение задачи сводится к построению горизонтальной проекции точки В Þ В1, т. е. надо определить разность удаления концов отрезка АВ до П2.
Как это можно сделать?
Только построив прямоугольный треугольник на П2 для этого информации?
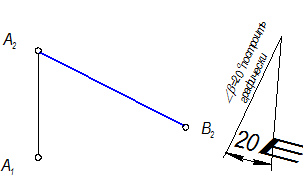
Да, т. к. есть один катет А2В2 и угол наклона гипотенузы к нему.
Провести линию связи из В2 т. к. В1-В2 находятся на одной линии связи. Провести из точки А вспомогательную прямую ^ А1А2 т. к. по условию точка В дальше от П2, чем точка А.
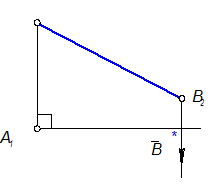
А2В2 - первый катет. Перпендикуляр (второй катет) можно проводить из любой точки А2 или В2.

Построить из точки А2 угол 20° (перенести графически) с помощью циркуля.
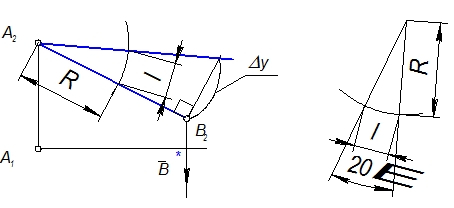
В2В0 (Dу) - второй катет. Гипотенуза А2В0 -натуральная величина отрезка АВ.
В2В0 - значение второго катета отложить от точки В Þ В1.
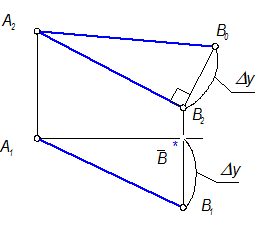
Задача №11
Через точку А провести прямую m ° n, если EÎ m, CÎ n, точка Е расположена перед С на 10мм.
Прямые m и n скрещивающиеся, значит у них нет общих точек. Точки Е и С - фронтально конкуририрующие, т. е. точки С и Е лежат на одном ^ к П2, поэтому С1 и Е1 лежат на одной линии связи.
|
|
|

Продлите линию связи из точки С1. От С1 отложите 10 мм ближе к наблюдателю Þ получим точку Е1

Через две точки А1 и Е1, проводим m1, точка Е(Е1) расположена ближе к наблюдателю, значит на П2 фронтальная проекция точки С(С2) - невидима, взять в скобки..

Точки D и F - горизонтально конкурирующие, построить их фронтальные проекции и определить видимость самостоятельно (Модуль №1, стр. 26).
|
|
|


