 |
Задача №47. Построение горизонтальной проекции точки А:. а) на П2 измеряем радиус R параллели точки А2;. Алгоритм построения.
|
|
|
|
Задача №47
Обвести плавной кривой линией правый полумеридиан (гиперболу), симметрично построить левый полумеридиан. Обвести фронтальную проекцию поверхности основной толстой линией.
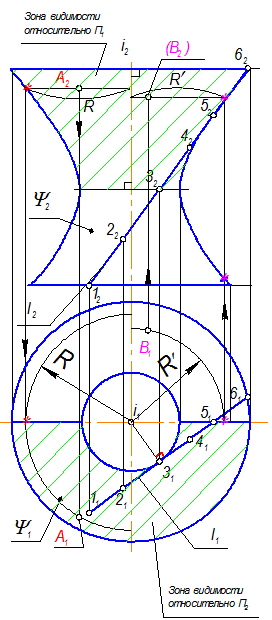
Для построения недостающих точек на поверхности гиперболоида, необходимо указать зоны видимости.
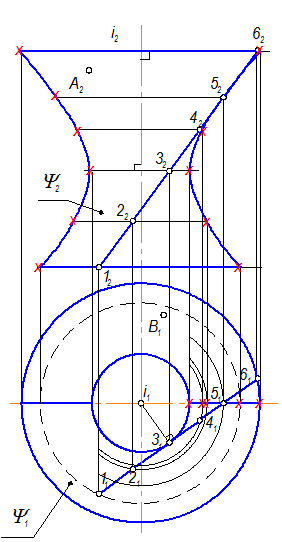
Построение горизонтальной проекции точки А:
а) на П2 измеряем радиус R параллели точки А2;
б) на П1 радиусом R проводим окружность и проецируем на нее точку А1 в заштрихованной зоне.
Построение фронтальной проекции точки В:
а) на П1 через точку В1 проведем параллель до пересечения с главным меридианом и отметим точку пересечение звездочкой (*), линия связи из этой точки пересечет фронтальную проекцию правой гиперболы в двух точках. Так как точка В1 - видимая, то точку выбираем в верхней части. Проведем параллель радиусом R’ и на пересечении линии связи от точки В1 и этой параллели построим точку В2, которая будет невидимой.
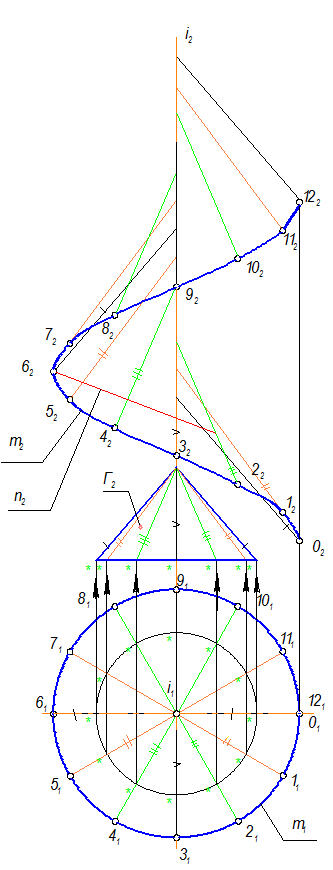
Задача №48
Построить проекции поверхности кольца L(i, l). Обозначить проекции горла n(n1, n2) и экватора m(m1, m2), а(а2), a1 =?
Каждая точка образующей на П2, вращаясь вокруг оси i2 опишет траекторию окружности - параллель, на П1 фронтальная проекция параллели проецируется в прямую линию ^ i.
Построение поверхности подробно описано в М2-37, 38

Достроить правый полумеридиан, симметрично ему построить левый. Обвести проекции поверхности основной толстой линией.

Отмечаем особые точки на а(а2): точки 1 и 2 принадлежат экватору, точки 3(4) и 5(6) ближней и дальней параллелям, 9(10) Ì образующей l. Точки 7(8) определят кратчайшее расстояние между ветвями кривой а, находим их через построение дополнительной параллели (точки К, L)
|
|
|

Отмечаем и простраиваем промежуточные точки.

Фронтальная проекция кривой а видима на П1 от точки 5 до точки 6 через точку 1.
Задача №50
Построить проекции поверхности косого геликоида S(i, m, Г), n(n2) Ì S, n1 =?
Алгоритм построения.
1. Направляющую винтовую линию m(m1m2) разделим на 12 точек и обозначим.
2. На П1 построим 12 проекций образующих, которые пересекут окружность направляющего конуса. Точки пересечения перенесем на фронтальную проекцию конуса и соединим с вершиной.
Фронтальные проекции образующих геликоида будут параллельны соответствующим образующим направляющего конуса.
3. Все линии, ограничивающие проекции поверхности и крайние образующие необходимо обвести. На П2 строим огибающую к семейству прямолинейных образующих.
4. Определяем видимость направляющей и образующих.
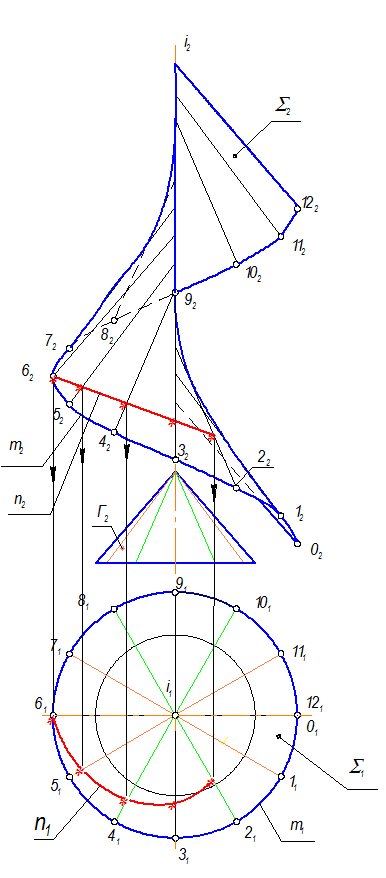
5. n(n2) Ì S. Для построения горизонтальной проекции n, на П2 отметим звездочками пересечения n2 с фронтальными проекциями образующих от точек 62, 52, 42, 32, 22.
6. Из этих точек проведем линии связи на соответствующие проекции образующих геликоида.
7. Соединим на П1 звездочки плавной кривой, получим горизонтальную проекция n(n1).
Модуль №3
Главные позиционные задачи
Решение задач по 1 и 2 алгоритмам
Задача №55
Построить проекции точки пересечения прямой с поверхностью: в Ç D.
Алгоритм построения.
в - фронтально проецирующая прямая.
D - конус вращения (поверхность непроецирующая)
1) в ^^ П2 Þ в2 = К2
2) К1 Î D
Горизонтальную проекцию К1 можно построить двумя способами:
1 способ: точка К принадлежит образующей SA(S2A2 Þ S1A1)

2 способ: точка К принадлежит параллели с(с2 Þ с1)
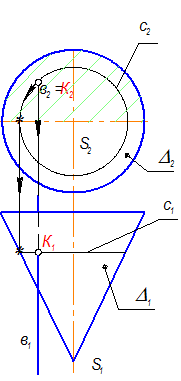
3) Определяем видимость прямой и поверхности конуса на П1.
4) На П2 при данном расположении конуса все точки видимы, в т. ч. и К2.
|
|
|


