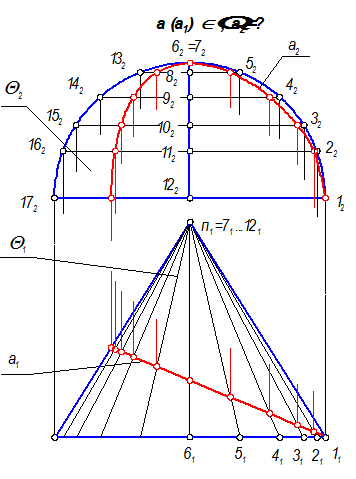
Задача №40. Построить проекции коноида Q(n,m,П1), а(а1) Ì Q, а2 = ? . Закон образования каркаса коноида l Ç m; l Ç n; l || П­1

Задача №40

Построить проекции цилиндроида L(n, m, Г), d(d₁) Ì L, d₂ =?

Задачу решить самостоятельно, учитывая положение плоскости параллелилизма.

 

Задача №41

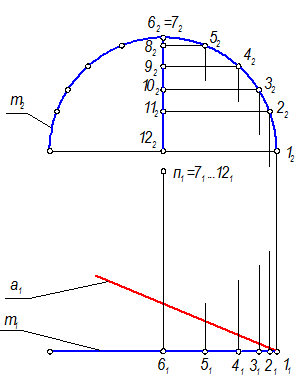
Построить проекции коноида Q(n, m, П₁), а(а₁) Ì Q, а₂ =?

Закон образования каркаса коноида l Ç m; l Ç n; l || П­₁

Какое положение занимают неподвижные направляющие m, n?

m(m₁, m₂) - плоская кривая, лежащая во фронтальной плоскости уровня.

n(n₁, n₂) - горизонтально проецирующая прямая

С какой проекции начинать построение? С фронтальной, т. к. l || П₁.

Проводим фронтальные проекции образующих, определяем положение точек на П₁, через которые пройдут горизонтальные проекции образующих.

Достраиваем и определяем видимость проекций поверхности.

Конкурирующих точек нет, поэтому проекции образующих видимы на П₁ и П₂

Для построения фронтальной проекции кривой а отмечают точки пересечения а(а₁) с горизонтальными проекциями образующих и строят их фронтальные проекции по принадлежности образующим, с помощью линий связи Фронтальная проекция кривой а(а₂) видима.

 

Задача №42

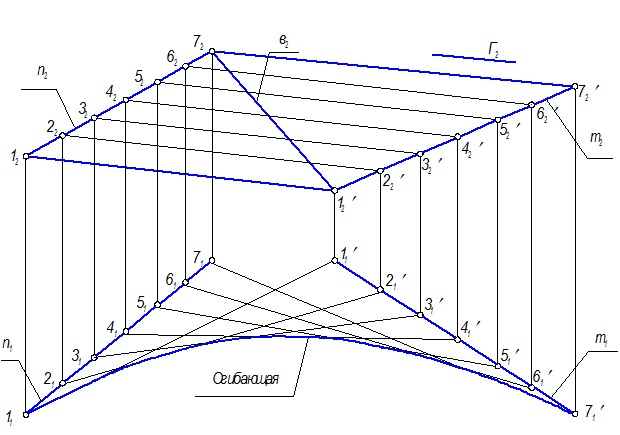
Построить проекции гиперболического параболоида (косой плоскости) S(n, m, Г), в(в₂) Ì S, в =?

Закон образования каркаса гиперболического параболоида (косой плоскости) l Ç m; l Ç m; l || Г

1. На П₂ разделим фронтальную проекцию направляющей n₂ на 7 точек.

2. Проведем через каждую точку проекцию образующей параллельно Г₂ – плоскости параллелизма.

3. На П₁ построим проекции точек и проведем проекции образующих через одноименные точки.

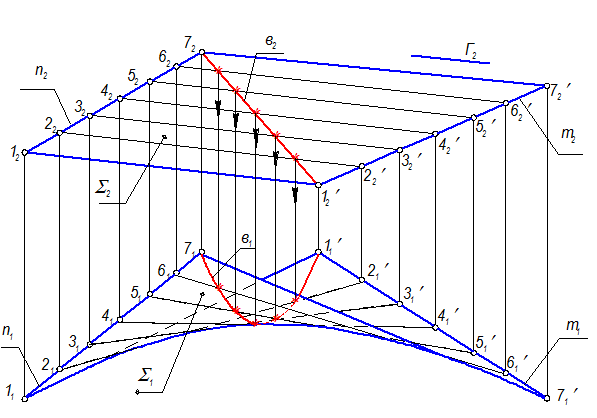
4. На П₁ определяем видимость поверхности: образующая 77’ - выше всех, она видна вся; образующая 66’ не видна только в одной точке, за 7 образующей; образующая 55’ не видна между 66’ и 77’; образующая 44’ не видна между 55’, 66’ и 77’; образующая 33’ не видна между 44’, 55’, 66’ и 77’; образующая 22’ не видна между 33’, 44’, 55’, 66’ и 77’; образующая 11’ не видна за всеми (от 2 до 7). Крайние проекции образующих (с учетом видимости) обвести основной линией.

MN – горизонтально конкурирующие точки

5. Для построения горизонтальной проекции линии в(в₁) отметим звездочками точки пересечения в(в₂) с фронтальными проекциями образующих поверхности. Проведем линии связи из этих точек на соответствующие горизонтальные проекции образующих.

6. С учетом видимости соединим точки (звездочки) и получаем горизонтальную проекцию кривой в(в₁).

 

Задача №43

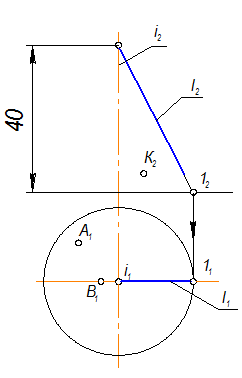
Построить проекции конуса вращения S(i, l), h = 40мм., А, В, К(А₁, В₁, К₁), А₂ =? В₂ =? К₂ =?

Алгоритм построения.

1. На П₂ от вершины конуса отложим высоту 40мм. определив положение основания (линию обреза) конуса..

2. Используя свойство симметрии поверхностей вращения, достраиваем левый полумеридиан.

3. Горизонтальная проекция - окружность R = l₁.

4. Видимость поверхности:

Все точки, принадлежащие конусу, на П₁ будут видимыми;

Видимость на П₂ ограничится главным (фронтальным) меридианом.

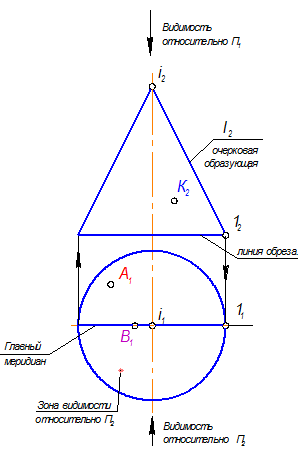
5. Чтобы определить недостающие проекции точек, нужно через имеющиеся проекции точек провести линии: образующую или параллель точки, радиусом от оси до очерка.

а) Для построения точки А(А₂) проведем проекции образующей и по принадлежности ей, с учетом видимости построим точки А(А₂).

б) Точка В принадлежит очерковой образующей, поэтому для построения точки В₂ достаточно провести от В₁ линию связи.

в) Построение точки К(К₁): через К(К₂) проведем радиусом R параллель (от оси до очерка).

Построить горизонтальную проекцию этой параллели. Линия связи, проведенная от точки К₂ дважды пересекает параллель, но точка К₁ будет располагаться в зоне видимости, т. к. относительно П₂ точка К₂ – видима.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: