 |
Задача №57. Алгоритм построения. a1 Ç m1 = 11 Þ 12 ; b1 Ç m1 = 21 Þ 22 Þ m2
|
|
|
|
Задача №57
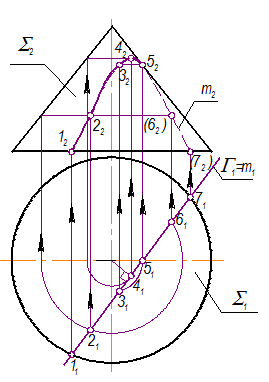
Построить проекции линии пересечения заданных плоскостей: S Ç Г(а || b) = m.
Алгоритм построения.
SÇ Г(a || b) = m(прямая); 2 ГПЗ, 2 алг.
1) S ^^ П1 Þ m1 =S1
2) m2 Ì Г
a1 Ç m1 = 11 Þ 12; b1 Ç m1 = 21 Þ 22 Þ m2

На П2 отрезок 1222(m2) будет фронтальной проекцией линии пересечения.

Задача №58
Построить проекции линии пересечения поверхностей с плоскостью: S Ç Г = m; L Ç Г = l1, l2

Построения проводим для каждой поверхности отдельно:
1. Цилиндрическая поверхность L Ç Г = l1, l2 (2 образующие цилиндра). Это 2 ГПЗ. Случай, когда обе фигуры проецирующие, но относительно одной и той же плоскости проекций (см. М3, стр. 24). Поэтому решаем эту часть задачи по 2 алгоритму.
Г - горизонтально проецирующая плоскость;
L - горизонтально проецирующая поверхность.
Общим элементом пересечения будут являться две образующие l1 и l2 – горизонтально проецирующие прямые.

Г ^^ П1; L ^^ П1 Þ l11 и l21 - точки
Находим фронтальные проекции образующих l(l1, l 2) по принадлежности L, с учётом видимости.

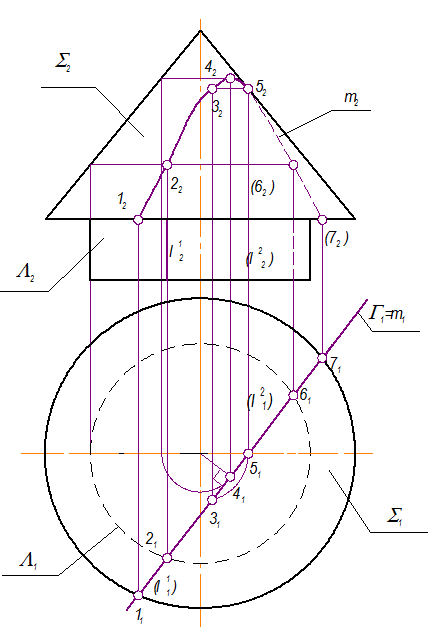
2. Конус S Ç Г = m (гипербола); 2 ГПЗ, 2 алг.
Эту задачу решаем точно так же, как описано в М3 стр. 13.
Г || П1 Þ m = Г1

На m1 возьмём 7 точек и строим их, как описано в М3-13.
а) Точки 1(11, 12) и 7(71, 72) расположены на основании конуса; точка 5(51, 52) - на очерковой образующей конуса, она определяет видимость гиперболы относительно П2, так как расположена в плоскости фронтального меридиана;
б) Точка 4(41, 42) - вершина гиперболы (41 - ближайшая к центру вращения);
в) Точка 2(21, 22) и 6(61, 62) - промежуточные, лежат на одной параллели; точка 3(31, 32) - промежуточная, лежит на одной параллели с точкой 5(51, 52).
г) Строим m2 с учётом видимости.
Общий вид решения задачи:
|
|
|
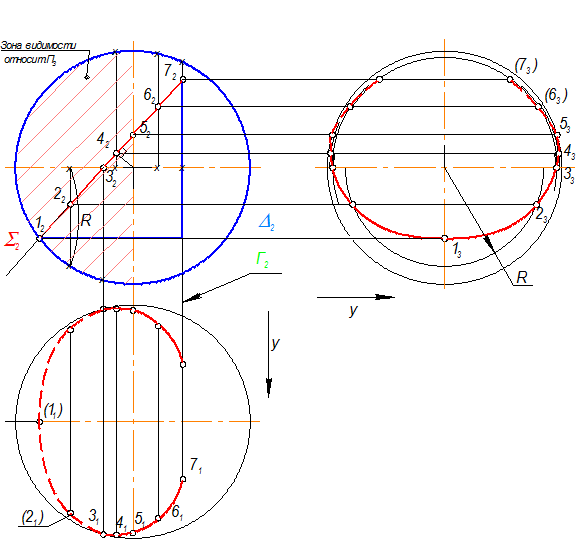
Задача №60
Построить три проекции шара со сквозным отверстием.

Эта задача является аналогом задачи, рассмотренной в М3, стр. 14-15, с той разницей, что в М3 пересекаются поверхности сферы и призмы, а в данной задаче - тело шара с призматическим вырезом; кроме того, в М3 призма – горизонтально проецирующая, а в данной задаче вырез имеет форму фронтально проецирующей призмы. Однако, принцип решения тот же.
Сквозное отверстие представляет собой фронтально проецирующую трехгранную призму. Каждая грань - это секущая плоскость на шаре.
Алгоритм построения разделим на три этапа:
1. Сечение шара плоскостью S(S2)
2. Сечение шара плоскостью D(D2)
3. Сечение шара плоскостью Г(Г2)
1 этап.
S(S2) - фронтально проецирующая пл-ть. При сечении этой плоскостью шара получаем кривую - эллипс на П1 и на П3.
На S2 возьмём 7 точек. Построения на П1 начинаем с характерных точек:
точка 1(12) принадлежит фронтальному меридиану Þ 11;
точка 3(32) принадлежит экватору и определяет видимость эллипса на П1 Þ 31.
Так как эллипс на П1 симметричен относительно плоскости фронтального меридиана, то точки на П1 будем обозначать только в одной полусфере.
Находим эти точки на П3. Точка 1(12) принадлежит профильному меридиану Þ 13 (относительно П3 – это характерная точка).

Достроив остальные профильные проекции точек с учетом видимости, соединим их, получим кривую неполного эллипса..
2 этап
D(D2) - горизонтальная плоскость уровня создает при сечении шара неполную окружность на П1 - невидимую, а на П3 окружность проецируется в прямую, видимую от точки 13 до точки 103 и невидимую часть от 103 до 93.

3 этап
Г(Г2) - профильная плоскость уровня при сечении шара создает:
на П3 - неполную окружность (невидимую);
на П1 проецируется в два отрезка видимых от 71 до 81 и невидимых от 81 до 91.
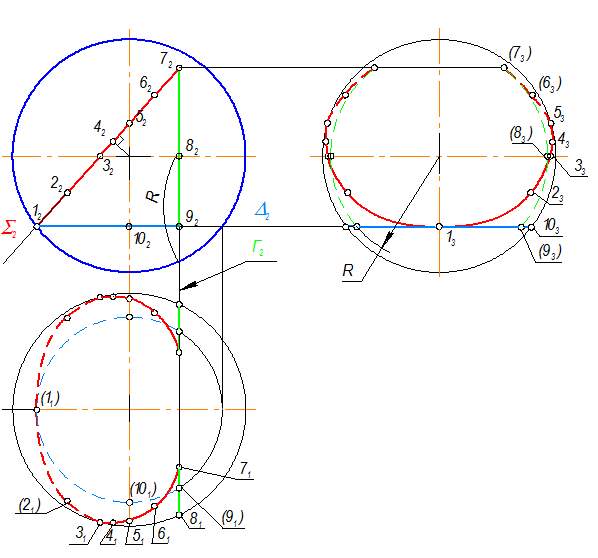
Уточняем контур видимых линий на П1 и П2.
|
|
|

|
|
|


