 |
Задача №34. Проекции геометрической части определителя. Строим дискретный каркас. С какой проекции начнем конструировать линейчатую поверхность? Можно начать с любой, но, учитывая условие задачи (высота 40 мм), начнем построение с фронтальной проекции, пр
|
|
|
|
Задача №34
Построить проекции трехгранной призмы Ф(АВС, s), М Î Ф, М1 =? Высота призмы 40 мм
Вспомним алгоритм конструирования поверхности: М2-15. Что задано на чертеже?
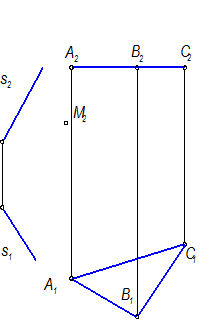
Проекции геометрической части определителя. Строим дискретный каркас, закон каркаса:
lÇ ABC, l || s
С какой проекции начнем конструировать линейчатую поверхность? Можно начать с любой, но, учитывая условие задачи (высота 40 мм), начнем построение с фронтальной проекции, проведя 3 образующие || s2.
Построить проекцию линии обреза на П2

А2’В2’С2’ - фронтальная проекция линии обреза. С помощью линий связи построить ее горизонтальную проекцию – А1’В1’С1’
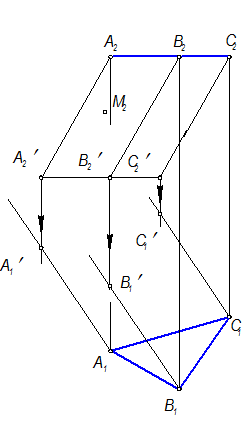
Для того, чтобы обвести проекции поверхности основной сплошной линией, необходимо определить видимость.
Точки 1 = 2(11 = 21) - горизонтально конкурирующие, точка 1 выше, чем точка 2.
Точки В’ = 4(В2’ = 42) - фронтально конкурирующие, точка В ближе к наблюдателю, чем точка 4.
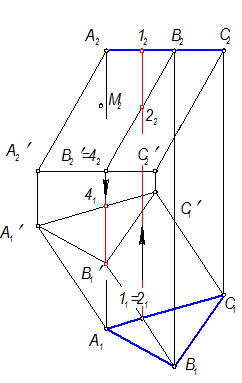
Ребро В1В1’ частично видимо, т. к. поверхность (в данном случае призма) - это пустотелая геометрическая фигура., имеющая только боковую поверхность.

На П2 точка М(М2)- видимая, Î АА’ВВ’. Через точку М(М2) провести образующую М5(М252). Точка М(М1) - невидимая.

Задача № 35
Построить проекции пирамидальной поверхности Г(1, 2, 3, S); А, В Î Г; А1, В2=?
Вспомним алгоритм конструирования поверхности: М2-15. Что задано на чертеже?

Проекции геометрической части определителя. Строим дискретный каркас из трех образующих, закон каркаса: l Ç 1, 2, 3; S Î l
Соединить точки направляющей 1, 2, 3 с вершиной S, на обоих проекциях. Определить видимость проекций поверхности, точки 4=5(42 =52) - фронтально конкурирующие точки, точки 6=7(62=72) - горизонтально конкурирующие точки.
|
|
|

Точка 7 выше, чем точка 6, точка 4 ближе к наблюдателю, чем точка 5.
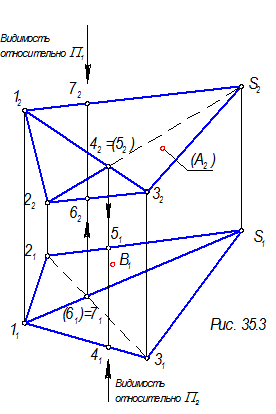
А Î Г, А1 =?

В Î Г, В2 =?

Задача №36
Построить проекции пирамидальной поверхности общего вида Y(А, В, С, D, F, S), n Ì Y, n1 =?
Задачу 36 решить самостоятельно, учитывая опыт решения предыдущих задач. Ломаную линию
n(n1) построить по принадлежности соответствующим граням, учитывая видимость проекций
поверхности.
Задача №37
Построить проекции конической поверхности общего вида Г(m, S), АÎ Г, ВÎ Г, А2 =?, В1 =?
Коническая поверхность - кривая линейчатая (М2-21, 22), образующая l - прямая линия.
Что задано на чертеже?
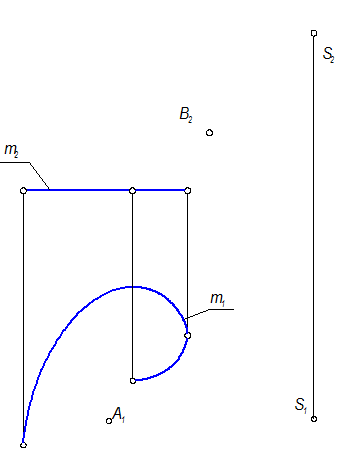
Проекции геометрической части определителя. Строим дискретный каркас, закон каркаса:
l Ç m; l É S
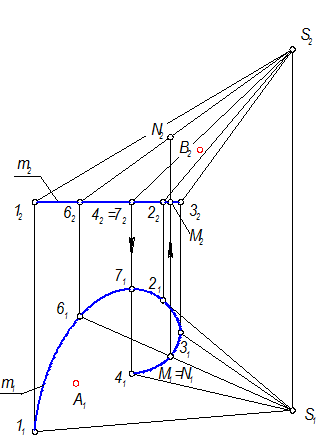
Провести конечное число образующих, начиная с очерковых.
Определить видимость проекций поверхности:
точки М=N(М1=N1) - горизонтально конкурирующие,
точки 4=7(42=72) - фронтально конкурирующие,
точка N выше, чем М,
точка 4 ближе к наблюдателю, чем точка 7

А, В Î Г, В1 =? А1 =?
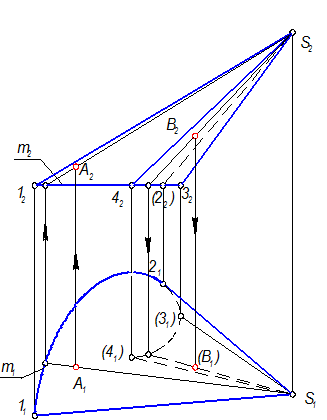
Через точки А и В провести образующие.
Задача №38
Построить проекции цилиндрической поверхности S(m, s).
h =35 мм, K Î S, K2 =?, N Î S, N1 =?
Алгоритм построения.
На чертеже заданы проекции геометрической части определителя цилиндрической линейчатой поверхности.
Закон образования каркаса цилиндрической поверхности: l Ç m, l || s
1. Расстояние между верхним и нижним основаниями равно 35 мм.
2. Через центр направляющей m проведем осевые линии параллельно s на П1 и на П2 Þ О1’, О2’
3. На направляющей m обозначим 4 точки с учетом видимости.

4. На П2 проведем две очерковые образующие: 11’(1212’) и 22’(2222’) || s2 и построим фронтальную проекцию цилиндра.
5. На П1 построим горизонтальную проекцию линии обреза Þ О’(О1’).
6. Прямая ЕС(Е1С1) É О ^ О’(О1’) определит положение касательных к основанию, которые будут очерковыми образующими на П1.
|
|
|
Определяем видимость:
7. Строим фронтальные проекции образующих: ЕЕ’ -видимая, СС’ невидимая.
8. На П1 строим проекции образующих
11’(1111’) и 44’(4141’) - видимые;
22’(2121’) и 33’(3131’) - частично видны через верхнюю линию обреза.
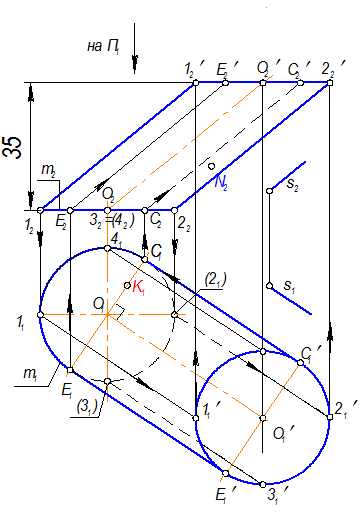
Построение К(К2).
Обозначим зону видимости относительно П2: все точки, расположенные на образующих от 1(11) до 2(21) через 3(31) на П2 будут видимы.
Через К(К1) проведем образующую || s1 Þ 6(61) Þ 6(62).
Через точку 6(62) проведем образующую || s2 Þ 6К(62K2)
На П1 образующая 6К(61К1) находится вне зоны видимости относительно П2, следовательно, фронтальная проекция точки К(К2) будет невидима.

Построение N(N1)
Обозначим зону видимости относительно П1: все точки, расположенные на образующих от Е(Е2) до С(С2) через 1(12) на П1 будут видимы.
N(N2) на П2 видима, следовательно горизонтальная проекция N(N1) должна располагаться в зоне видимости относительно П2, т. е. точка 51 - ближе к наблюдателю.
Проводим образующую N5(N252) || s2 Þ 5(51) Þ (51N1), т. к. точка N2 - вне зоны видимости относительно П1, то точка N1 должна быть невидимой, но, поскольку у цилиндра только боковая поверхность и он пустотелый, то точка N1 - видима, т. к. частично образующая 51N1 видна, и как раз на видимую часть этой образующей проецируется точка N(N1) - видимая.

|
|
|


