 |
Задача №20. Сторона АВ || h, точка А принадлежит f. A2 Î f2 Þ A1 Î f , A2B2 || h2 Þ A1B1 || h1 (Рис
|
|
|
|
Задача №20
Дана плоскость L(h Ç f), АВС Ì L, А1В1С1 =?
Как построить А1В1С1, зная свойство принадлежности точки и прямой к плоскости? Треугольник АВС надо рассматривать, как фигуру, состоящую из вершин (точек А, В, С) и сторон (отрезков прямых), т. е. следует применить решение предыдущих задач №17 и №18.

Рис. 20-1
Сторона АВ || h, точка А принадлежит f.
A2 Î f2 Þ A1 Î f, A2B2 || h2 Þ A1B1 || h1 (Рис. 20-2)
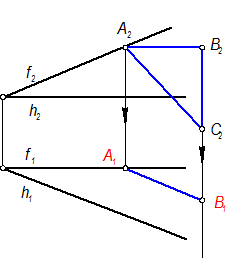
Рис. 20-2
Горизонтальная проекция АС строится по двум точкам: А и 1 = А2C2 Ç h2 Þ 11 Þ С1 (Рис. 20-3)
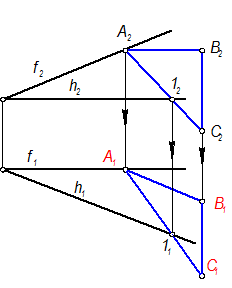
Рис. 20-3
Задача №21
Задача решается аналогично, чтобы построить фронтальные проекции точек D, F, E, необходимо построить фронтальные проекци любых двух сторон треугольника (например DF и DE), исходя из свойства принадлежности прямой к плоскости. Для чего следует их продлить до пересечения с Ф, т. е. с m1 и n1.
Задача №22
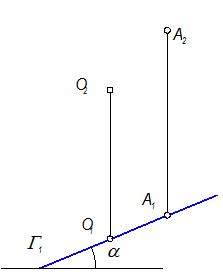
Определить угол наклона плоскости S(g) к П1
А(А2) Î S. А1 =? Ð a =?
Плоскость S задана g - линией ската, но т. к. положение g в плоскости определяется положением горизонтали этой плоскости, то значит можно однозначно утверждать, что данная плоскость задана двумя пересекающимися прямыми Þ S(g) = S(g Ç h) (Модуль №2, стр. 8)

g ^ h Þ h2 ^ линиям связи, g1 ^ h1, h2 провести через А2, А1 находится по принадлежности
горизонтали
Но как определить угол a?
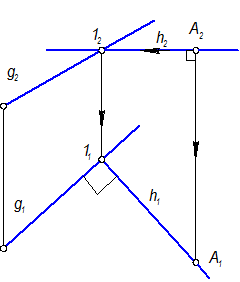
Угол a между g u g1 - есть угол наклона S Ù П1 = g Ù g
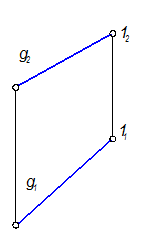
g(g1, g2) - прямая общего положения
Для определения угла (a) необходима истинная величина линии ската, которую определим методом прямоугольного треугольника (задача №8)

Угол между g и g1 = Ð a.
Если бы не требовалось определить А1, то угол можно было бы определить и без построения горизонтали. Достаточно задаться любым отрезком на линии ската.
|
|
|

Задача №23
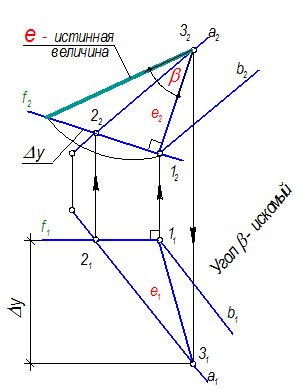
Определить угол наклона плоскости Ф(а || b) к П2. Ð b =?
Как определить е - линию наибольшего наклона плоскости Ф к П2(е ^ f Þ е2 ^ f2)? Задача графически сложная, но легко решается, если ее разбить на три этапа (на три задачи), которые встречались на предыдущих страницах:

1) Построить проекции фронтали f (f1 f2)

Построить f(f1, f2): f1 ^ линиям связи (в любом месте f1 Ç а || в), f2 по принадлежности плоскости Ф
2) Построить проекции линии наибольшего наклона е(е1 е2)

Построить е(е ^ f) Þ е2 ^ f2. Построить е2 можно бесконечное множество.

Выбираем наиболее рациональный вариант и достраиваем е(е1) Ì Ф (по двум точкам 1 и 3).
3) Определить натуральную величину | е| с помощью прямоугольного треугольника. Угол Ð b = между е – е2 (Ф Ù П2 = е Ù е2)

е(е1, е2) – прямая общего положения

Задача №24
Эта задача решается аналогично, только алгоритм нужно применить относительно П1.
Задача №25
Окружность k Ì Г(Г1), A Î k, O - центр окружности.
Построить: k1 =?, k2 =?
Плоскость Г занимает горизонтально проецирующее положение. Г1 = главная проекция, обладающая собирательными свойствами, поэтому k1 - прямая линия совпадающая с Г1. Г имеет угол (a) наклона к П2, поэтому окружность спроецируется на П2 с искажением, в виде эллипса.
При этом, какое положение займут большая и малая оси эллипса?
Чтобы построить а2 и в2, нужно знать значение радиуса окружности (R), т. к. а1 = 2´ R, в2 = 2´ R.

Точка А принадлежит окружности, поэтому соединив точку А с О Þ R. На какой проекции можно замерить значение радиуса?

Нигде! Т. к. ОА - прямая общего положения.
Методом прямоугольного треугольника определяем натуральную величину радиуса окружности Þ R

а (1, 2) - малая ось эллипса
в (3, 4) - большая ось эллипса

Эллипс - центрально симметричная замкнутая кривая, следовательно относительно точки О2 на кривой таких точек как А2 - четыре.
|
|
|
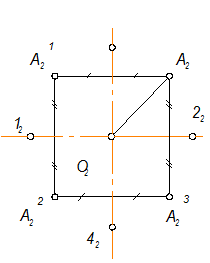
Теперь плавной кривой соединяем все 8 точек.

Плавной кривой соединить все точки
|
|
|


