 |
Задача №46. Возьмем на образующей l(l1,l2) 6 точек.
|
|
|
|
Задача №46
Построить проекции поверхности вращения общего вида Ф(i, l). Достроить недостающие проекции точек А, В, С.
В этой задаче проекции образующей l(l1, l2) не лежат в плоскости фронтального меридиана, поэтому нам необходимо повернуть образующую так, чтобы она легла в одну плоскость с осью вращения (М2 ст. 29)
Каждая точка образующей на П1, вращаясь вокруг оси i1, опишет траекторию окружности - параллель, на П2 ее проекция проецируется в прямую линию ^ i2.
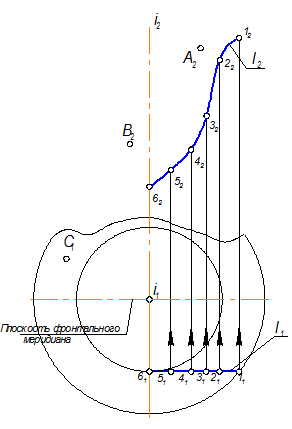
Возьмем на образующей l(l1, l2) 6 точек.

Введем каждую точку в плоскость фронтального меридиана. Например, точка 1 опишет наибольшую, верхнюю параллель(экватор), точка 6 - наименьшую, нижнюю параллель (горло).

Аналогичные построения проведем с оставшимися точками Þ правый полумеридиан.

Симметрично правому полумеридиану достраиваем левый. Обводим основной толстой линией проекции поверхности.

Для построения недостающих проекций точек А, В, и С необходимо определить зоны видимости:
1) Все точки, принадлежащие поверхности, относительно П1 будут видимы (изнутри).
2) Видимость относительно П2 показана заштрихованной зоной.
а) Для построения горизонтальной проекции точки А(А1) необходимо:
- через точку А2 провести параллель радиусом R (от оси до очерка);
- на П1 строим проекцию этой параллели радиусом R;
- проводим линию связи от точки А2 до пересечения с параллелью в заштрихованной зоне, т. к. точка А2 - видима;
- проекция точки А(А1) будет видимой.
б) Для построения точки В(В1) проводим аналогичные построения.
в) Построение фронтальной проекции точки С(С2):

Горизонтальная проекция точки С1 расположена в незаштрихованной зоне, т. е. за плоскостью фронтального меридиана, следовательно, фронтальная проекция точки будет невидимой.
|
|
|
На П1 через точку С1 проведем параллель радиусом R’’ до пересечения с горизонтальной проекцией левого полумеридиана в точке, которую обозначим звездочкой.
Построим фронтальную проекцию этой точки и проведем через нее фронтальную проекцию параллели, которой и будет принадлежать точка С2.
Задача №47
Построить проекции поверхности гиперболоида вращения Y(i, l), А, В(А2, В1), А1 =?, В2 =?
Алгоритм построения поверхности подробно расписан в М2 ст. 35, 36. Как и в предыдущей задаче №46, необходимо построить фронтальную проекцию правого полумеридиана (в данном случае гиперболу). Значит ввести все точки образующей - l в плоскость фронтального (главного) меридиана, тогда на П2 гипербола спроецируется без искажения.

Распределить точки на l(l1), которые определят положение будущих параллелей на П1 и П2:
Точка 1(11) - определит положение нижней параллели
Точка 3(31) - определит положение горла
Точка 6(61) - определит положение верхней параллели (экватора)
Точка 5(51) - уже принадлежит главному меридиану
Точки 2, 4, (21, 41) - промежуточные точки;
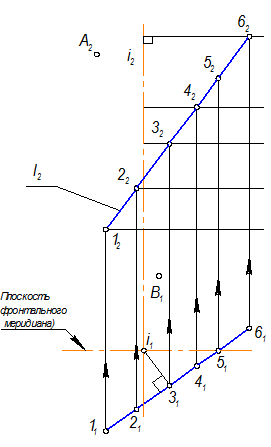
Через фронтальные проекции точек провести прямые ^ l2, которые определят положение фронтальных проекций параллелей.

Ввести точки (1... 6) в плоскость фронтального меридиана, а из них поднять линии связи, определяя положение соответствующих параллелей на П2.
На П2: верхнее и нижнее основания можно сразу вычертить основной линией - это линии обреза поверхности.
На П1: окружности верхнего основания и горла вычертить основной линией, а окружность нижнего основания штриховой линией, т. к. она закрыта верхней параллелью (экватором).
|
|
|


