 |
Задача №13. Для построения проекций плоской кривой применяется метод хорд. Модуль №2. Плоскость. Строим хорду АВ на П1 и П2. На П2 строим фронтальную проекцию хорды 12С2.
|
|
|
|
Задача №13
Построить горизонтальную проекцию плоской кривой m.
11 =?, 21 =?, m1 =?

Для построения проекций плоской кривой применяется метод хорд. Кривая считается плоской, если проекции точки пересечения проекций одноименных хорд лежат на одной линии связи (Модуль №1, стр. 29).

Строим хорду АВ на П1 и П2. На П2 строим фронтальную проекцию хорды 12С2.
А2В2 Ç 12С2 = 32

Опустив линию связи из точки 32, находим точку 31. Точка 3(32, 31) позволит построить горизонтальную проекцию хорды 1С.

Проводим линию связи из точки 12 до пересечения с продленной прямой 31С1 Þ 11

Плавной кривой соединим точки А1, 11, В1, получаем часть горизонтальной проекции кривой m.

Аналогично, строится точка 21.

Объединим все построения на одном чертеже, обозначим горизонтальную проекцию кривой m1.
Чем больше точек брать на кривой АВ, тем точнее построение (5-6 точек).
Задача №12
Определить взаимное положение отрезков прямых АВ и CD.

На 3-х картинном чертеже Монжа размеры по оси y (размеры ширины) на П1 и П3 остаются неизменными.
Точка С3 в системе П2- П3 (на линии связи ^ оси Z), взята произвольно, т. к. чертеж безосный. Все остальные проекции точек А, В, D на П3 жестко связаны с точкой С3
(Модуль №1, стр. 15).

Построение точки D3

Построение точки В3

Построение точки А3

Решение задачи 14 см. Модуль №1, стр. 31.
Решение задачи 15 см. Модуль №1, стр. 34
Модуль №2
Плоскость
Задача №17
В плоскости достроить недостающие проекции точки и прямой:
S(АВС) É l(l2); l =?; D(D ); D =?
В основе решения задачи лежит свойство принадлежности точки и прямой плоскости
(Модуль №2, стр. 2).
l Ì S, значит проходит через две точки этой плоскости 1 и 2.
|
|
|
точка 1 Î АВ, 12 Î А2В2 Þ 11 Î А1В1
точка 2 Î АС, 22 Î А2С2 Þ 21 Î А1С1

1. Построим горизонтальные проекции точек 1 и 2(с помощью линий связи) Þ 11 и 21
2. Через точки 1 и 2 проведем горизонтальную проекцию прямой – l.
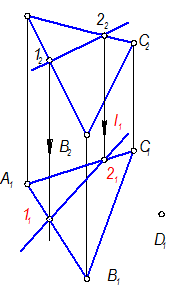
Очень важно не перепутать принадлежность точек своим отрезкам.
Как построить точку D?
Заметим, что точка D находится за пределами треугольника, но, тем не менее, принадлежит плоскости S, т. к. любая плоскость безгранична в пространстве, треугольник - это только ее определитель, с помощью которого она задана.
Так с чего начать? Обычно студенты предлагают провести линию связи из точки D1. Действительно D1 и D2 находятся на одной линии связи, Хорошо, провели, а дальше?
Исходя из свойства принадлежности точки плоскости, через точку D(D1) нужно провести вспомогательную прямую в плоскости. Сколько таких прямых можно провести? Бесчисленное множество, выбрав наиболее рациональный вариант.
1 вариант

2 вариант

Первый вариант рациональнее, т. к. для вспомогательной прямой нужно строить меньше точек (достаточно построить точку 3, точка А уже есть).
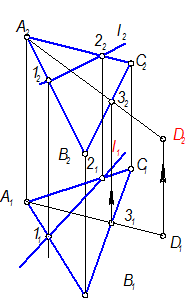
Задача №18
В плоскости достроить недостающие проекции линий:
Г(a || b), l(l2) Ì Г, l1 =?, m(m1) Ì Г, m2 =?
Принадлежность прямой плоскости, в случае, когда она проходит через две точки этой плоскости, была рассмотрена в задаче № 17. В этой задаче проиллюстрируем принадлежность прямой плоскости, если она проходит через одну точку плоскости и параллельна какой-либо прямой, лежащей в плоскости.
l1 =? l || a || b
Где взять эту точку? На l2 можно взять любую точку и построить ее проекции на П1 по принадлежности к Г (рис. 18. 1). Рациональнее взять точку 32 (рис. 18. 3).
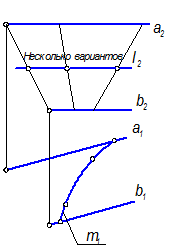
Рис. 18-1
Через прямую 1-2 строим проекции точки 3

Рис. 18-2
Теперь через точку 31 проводим l1 || а1 и в1

Рис. 18-3
Как построить m2?
Следует отметить, что для построения кривой m2 нужно взять не менее четырех точек.
|
|
|

Рис. 18-4
Точки 4, 6, 8 строятся без дополнительных построений, с помощью линий связи.

Рис. 18-5
Для построения точки 5 и 7 проводят дополнительные прямые || а и в.

Рис. 18-6
Находим точки 52, 72.
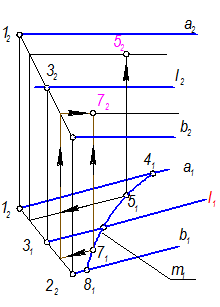
Рис. 18-7
Все точки соединить плавной кривой Þ m2

Рис. 18-8
|
|
|


