 |
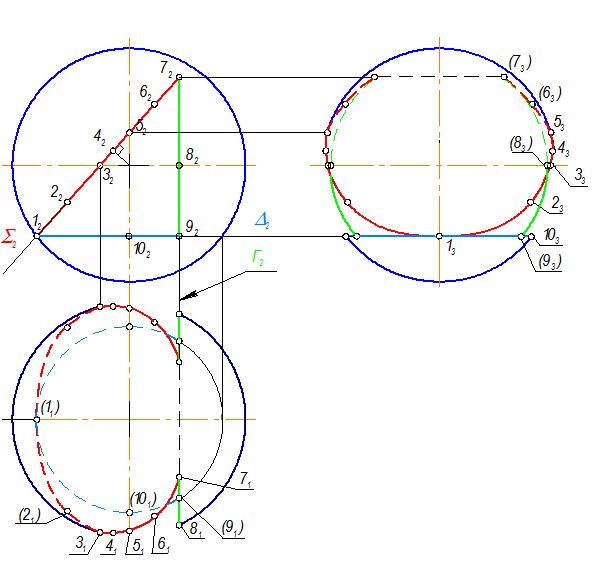
Задача №61. Алгоритм решения. Уточняем контур видимых линий на П1 и П3.
|
|
|
|
3 этап
Г(Г2) - профильная плоскость уровня при сечении шара создает:
на П3 - неполную окружность (невидимую);
на П1 проецируется в два отрезка видимых от 71 до 81 и невидимых от 81 до 91.

Уточняем контур видимых линий на П1 и П3.
Задача №61
Построить проекции линии пересечения поверхностей: S Ç L = m.
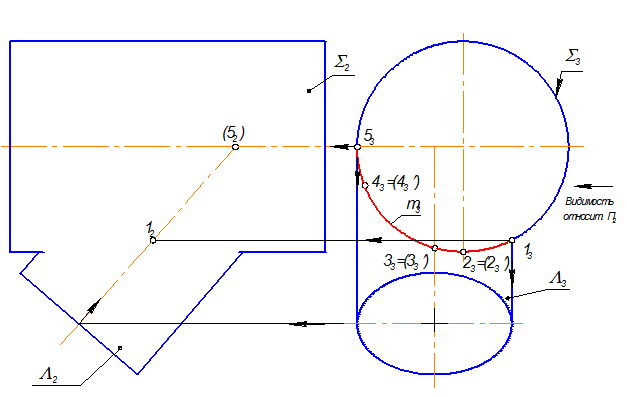
Алгоритм решения
Пересекаются два цилиндра Þ это 2 ГПЗ, характер пересечения - вмятие Þ общий элемент - одна пространственная кривая m. Цилиндр - профильно проецирующий, цилиндр – общего положения Þ решаем по 2 алгоритму: S ^^ П3 Þ m3 = S3; m2 Ì L
1. На m3 возьмём несколько точек
2. Точки 1(13) и 5(53) принадлежат профильным образующим цилиндра L Þ 12, 52 (невидима).
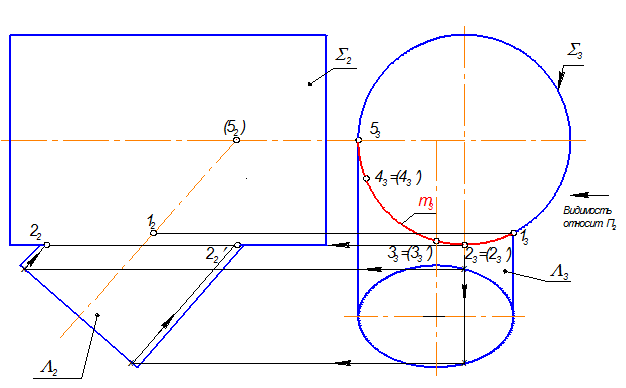
3. Точки 2(23 и 23') принадлежат фронтальному меридиану цилиндра S и определяют видимость кривой m относительно П2 Þ 22, 22'.
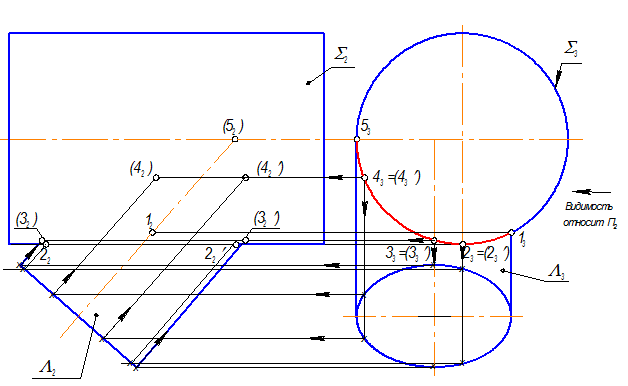
4. Построение фронтальных проекций точек 32, 32’, 42, 42’, которые на П2 будут невидимыми.

5. На П2 соединим точки с учетом видимости и получим фронтальную проекцию кривой m2.
Задача №64
Построить проекции линии пересечения поверхности призмы Ф(Ф1, Ф2) с плоскостью Г(h Ç f).
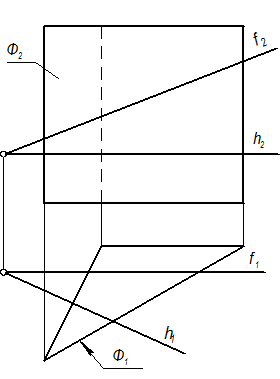
Результат пересечения - треугольник АВС.

Алгоритм решения:
Призма - горизонтально проецирующая, плоскость - общего положения Þ 2 ГПЗ, 2 алг.
Ф ^^ П1 Þ А1В1С1 = Ф1. А2В2С2 Ì Г.
Задача имеет несколько вариантов решения. Выберем самый оптимальный.
1. Сторона треугольника АС(А1С1) пересекается с горизонталью и фронталью плоскости Г в точках 1(11) и 2(21) Þ 12 и 22, проведём через эти точки А2С2.
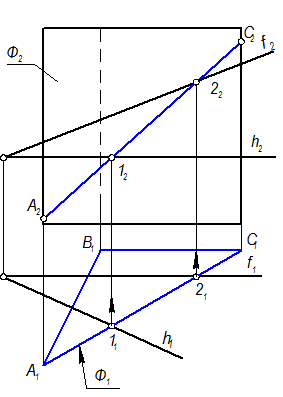
2. В1С1 || f1 Þ B2C2 || f2, проводим В2С2 с учётом видимости. Грань, на которой расположена сторона ВС, на П2 невидима Þ В2С2 - невидима.
3. По тем же причинам невидима сторона А2В2.
|
|
|
Подумайте, как можно ещё решить эту задачу. Сколько способов решения вы насчитали?
Задача №67
Построить проекции линии пересечения цилиндра с поверхностью полукольца: Г Ç Ф = в.
Пересекаются две поверхности вращения Þ результат пересечения - пространственная кривая; характер пересечения - вмятие Þ кривая линия - одна.
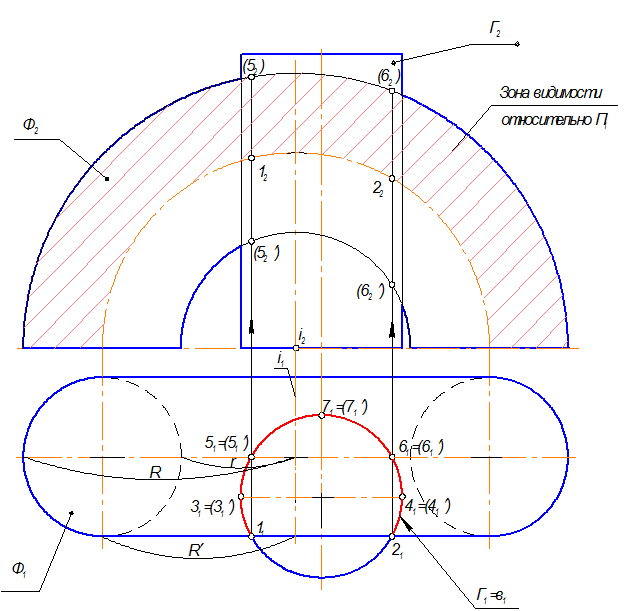
Алгоритм решения
Г Ç Ф = в, 2 ГПЗ
Г ^ П1, Ф – непроецирующая Þ 2 алгоритм
Г ^^ П1 Þ в1 = Г1; в2 Ì Ф
На проекции кривой в1 возьмём несколько точек. Видимость проекций этих точек на П2 определяется плоскостью фронтального меридиана цилиндра.
1. Точки 1(11) и 2(21) принадлежат ближней параллели полукольца радиусом R’ Þ 12 и 22 находим без дополнительных построений по принадлежности этой параллели. 12 и 22 - видимые.
2. Точки 51 и 61 (видимые на П1) принадлежат окружности R-экватору, на П2 точки 52 и 62 не видны; точки 51’ и 61’(невидимы на П1) лежат на окружности горла r, на П2 точки 52’ и 62’ - невидимые.
Обратите внимание! Мы построили проекции точек, лежащих на главных параллелях полукольца без вспомогательных построений, пользуясь только линиями связи.
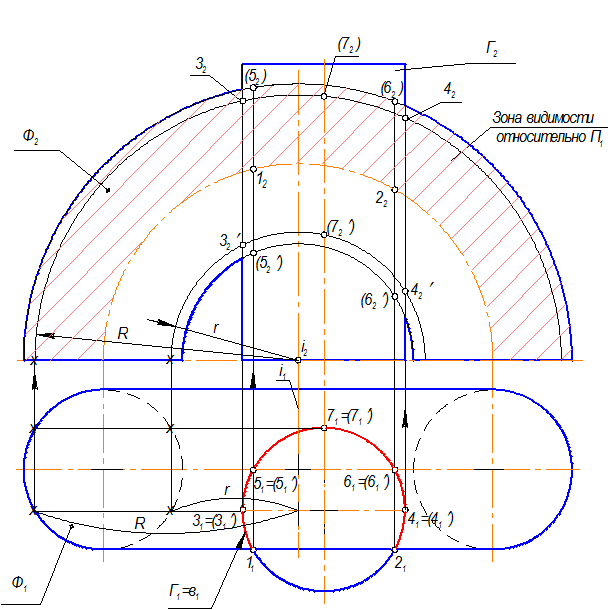
3. Горизонтальные проекции точек 31, 31’, 41, 41’ лежат в плоскости фронтального меридиана цилиндра, которая является границей видимости линии пересечения относительно П2. Проведем параллели через эти точки: радиусом R - для точек 31 и 41; радиусом r - для точек 31’ и 41’.
На П2 на пересечении параллелей и линий связи получим фронтальные проекции этих точек, которые будут видимыми.
4. Точки 71 и 71’ лежат на параллелях тех же радиусов, но на П2 будут невидимы.
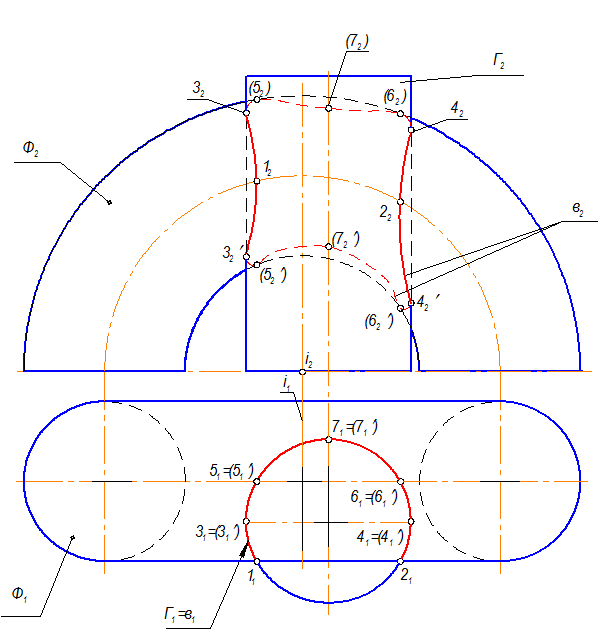
5. С учетом видимости проекций точек на П2 проведем кривую - фронтальную проекцию линии пересечения полукольца и цилиндра – в2.
6. На П2 окончательный этап построения заключается в обводке видимого и невидимого контуров полукольца и цилиндра.
|
|
|
|
|
|


