 |
Задача №71. Алгоритм построения. d Ç W = А,В ( две точки ) 1 ГПЗ, 3 алгоритм . 1. Для решения задачи необходимо взять вспомогательную плоскость - посредник S.
|
|
|
|
Задача №71
Построить проекции точек пересечения прямой с поверхностью: d Ç W = А, В.

Алгоритм построения.
d Ç W = А, В ( две точки ) 1 ГПЗ, 3 алгоритм
1. Для решения задачи необходимо взять вспомогательную плоскость - посредник S.
S ^^ П2; S É d Þ S2 = d2
2. Теперь в пересечении участвуют плоскость S и поверхностьW, причем плоскость - фронтально проецирующая.
S Ç W = в (плоская кривая второго порядка - эллипс. ) 2 ГПЗ, 2 алгоритм.
S ^^ П2 Þ в2 = S2; в1 Ì W
Построение горизонтальной проекции кривой в1:
а) На П2 плоскость - посредник S2 пересекает проекции всех образующих цилиндра. Сначала построим точки на очерковых образующих цилиндра - 1(12) и 2(22). Находим горизонтальные проекции образующих с учетом видимости и соответствующие проекции точек на них - 11 и 21.
Обратите внимание: точка 21 должна быть невидимой, но нам она видна через верхнее отверстие, т. к. у цилиндрической поверхности нет плоскостей оснований.
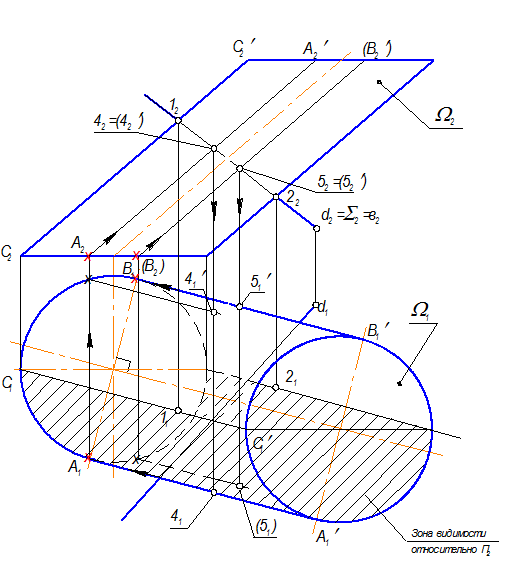
б) Видимость относительно П1 определяется точками, лежащими на образующих АА’, ВВ’.
Чтобы найти эти точки, произведём следующее:
1. Определим положение этих образующих на П2;
2. Найдём точки пересечения этих образующих с S2: 42, 42’, 52, 52’.
3. Находим горизонтальные проекции этих точек: 41 и 51’ - вершинные точки, лежащие на очерковых образующих, и 41’ и (51), лежащие на промежуточных образующих.
4. Таким образом, видимость относительно П1 определится участком цилиндра от образующей АА’(А2А2’) до ВВ’(В2В2’) через СС’(С2С2’).
в) Для построения кривой в1 - эллипса найденных точек недостаточно, поэтому на П2 возьмем произвольно еще 3 пары точек: 3(32, 32’), 6(62, 62’) и 7(72, 72’).
На П1 точки 31’, 61 и 61’ будут видимые;
точки 31 и 71’ - невидимые,
|
|
|
точка 71 - видимая через отверстие сверху.
г) С учетом видимости на П1 соединим точки и получим кривую в1
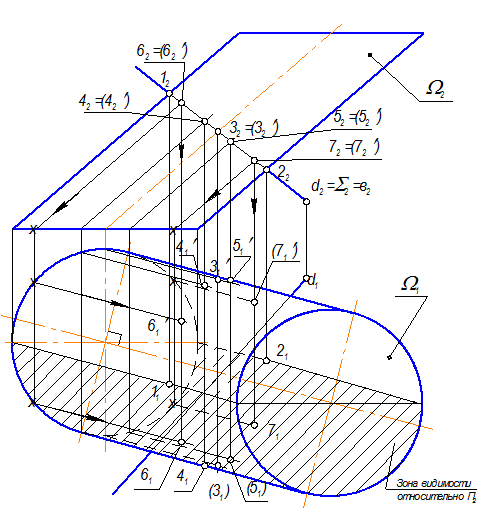
3. Там, где в1 Ç d1 = А1, В1 причем точка В1 - невидимая. С помощью линий связи находим фронтальные проекции точек А2, В2, причем, точка В2 - невидима.
4. Уточняем видимость прямой d на П1 и П2. Горизонтальная проекция прямой d1 до точки А1 - видимая, внутри невидимая и будет видна только после очерковой цилиндра. Видимость фронтальной проекции прямой d: от точки А2 до 22 - не видна.

Задача №73
Построить проекции линии пересечения:
АВС Ç DEF = MN (прямая) 2 ГПЗ, 3 алгоритм.
MN - прямая, для построения которой необходимо иметь две точки, поэтому возьмём две плоскости-посредника: Г2 и Г2’, которые выгодно провести через две стороны любого из треугольников. Проведём Г(Г2) через сторону DF(D2F2).
Алгоритм построения
1. Г Ç АВС = 1, 2 (прямая) 2 ГПЗ, 2 алгоритм.
Г ^^ П2 Þ 12, 22 = Г2
11, 21 Ì АВС.
Там, где 11, 21 Ç D1F1 = M1 Þ M2 Ì D2F2

Определили первую точку М(М1, М2)
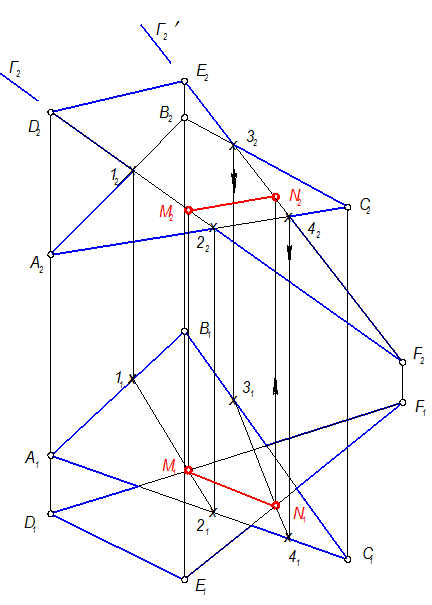
2. Нахождение второй точки N(N1, N2)
Г’(Г2’) = ЕF(E2F2);
Г’ Ç АВС = 3, 4 (прямая)
2 ГПЗ, 2 алгоритм
Г’ ^^ П2 Þ 32, 42 = Г2’
3141 Ì АBC.
Там, где 31, 41 Ç E1F1 = N1 Þ N2 Ì E2F2

Линия пересечения фигур MN - построена. Следующий этап решения - видимость пересекающихся плоскостей. Возьмём фронтально конкурирующие точки 1 и 5 и определим видимость D2M2. На П1 точка 51 расположена ближе точки 11, следовательно, D2M2 - видимая, а также видна E2N2
Для определения видимости на П1 отрезков Е1N1 и скрещивающегося с ним А1С1 достаточно посмотреть на П2 по стрелке Л: прямая Е2N2 выше, чем прямая А2С2, следовательно, отрезок Е1N1, а также и отрезок D1М1 - видимые.
Задача №76
Построить проекции линии пересечения поверхностей вращения: D Ç L= m, n.
Алгоритм построения
D Ç L = m, n (2 плоские кривые-эллипсы) (по теореме Монжа)
А и В - точки двойного соприкосновения.
|
|
|
1. Построение горизонтальной проекции эллипса – n1. На П2 на линии n2 возьмем несколько точек и найдем их горизонтальные проекции по принадлежности конусу D.
С учетом видимости соединим точки плавной кривой Þ n1.

2. Построение горизонтальной проекции эллипса – m1. Возьмём на m2 несколько точек и найдем их горизонтальные проекции по принадлежности конусу D. Соединяя их с учетом видимости, построим m1

Внимание! Построение эллипсов на конусе подробно описано в М3, стр. М3-10, М3-11.
|
|
|


