 |
Задача №78. Модуль №4. Метрические задачи. Задачи в рабочей тетради на странице 37 графически решаются просто. Задачи на определение расстояний между геометрическими фигурами (Модуль 4, стр
|
|
|
|
Задача №78
Построить три проекции конуса с призматическим вырезом, на виде слева совместить половину вида с половиной разреза.

Модуль №4
Метрические задачи
Задачи в рабочей тетради на странице 37 графически решаются просто. Такие задачи приводятся для того, чтобы Вы обратили особое внимание на их решение, т. к. в дальнейших сложных (конструктивных) задачах эти решения будут определять " решающее положение оригинала" (Модуль 4, ст. 23).
Задачи на определение расстояний между геометрическими фигурами (Модуль 4, стр. 8)
К таким задачам относятся: задачи на определение расстояний от точки до прямой, до плоскости, до поверхности; между параллельными и скрещивающимися прямыми; между параллельными плоскостями и т. п.
Все эти задачи объединяют три обстоятельства:
во-первых, поскольку кратчайшим расстоянием между такими фигурами является перпендикуляр, то все они сводятся к построению взаимно перпендикулярных прямой и плоскости.
во-вторых, в каждой из этих задач необходимо определять натуральную длину отрезка, то есть решать вторую основную метрическую задачу.
в-третьих, это сложные по составу задачи, они решаются в несколько этапов, и на каждом этапе решается отдельная, небольшая конкретная задача.
Задача №81
Определить расстояние между прямыми. Прямые а и в занимают положение горизонтально проецирующих прямых
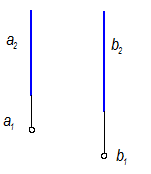
Расстояние между прямыми - это перпендикуляр n(n1, n2).

n - горизонталь, т. к. а и в ^ П1, но n ^ а и в, значит n || П1.

Решающее положение для определения расстояния между параллельными прямыми.
Горизонтальная проекция n Þ n1 есть искомая величина, т. к. перпендикуляр занимает положение горизонтали.
|
|
|
Задача №82
Определить расстояние между прямыми. Прямые с и d параллельны и занимают положение фронталей.

Расстояние между прямыми - это перпендикуляр n(n1, n2).

Начинаем построение с n2 (теорема о проецировании прямого угла), n2 ^ с2, d2 Þ n1
Натуральной величины на чертеже нет, т. к. n(n1, n2) – прямая общего положения

Определяем n методом прямоугольного треугольника.
Задача №83
Определить расстояние между прямыми. Прямые: l - горизонтально проецирующая, m - общего положения.
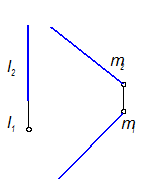
Расстояние между прямыми - это перпендикуляр n(n1, n2).

Т. к. l ^^ П1, то перпендикуляр к ней - есть горизонталь, и по теореме о проецировании прямого угла проводим n1 ^ m1, n Ç m Þ 1(11).

Решающее положение для определения расстояния между прямыми.
Горизонтальная проекция n Þ n1 есть искомая величина.
Задача №84
Определить расстояние от точки до прямой:

Расстояние между точкой и прямой - это перпендикуляр n(n1, n2).

Решающее положение для определения расстояния между точкой и прямой.
Горизонтальная проекция n Þ n1 есть искомая величина, т. к. перпендикуляр занимает положение горизонтали (аналогично заданию №81)
Задача №85
Определить расстояние от точки до прямой
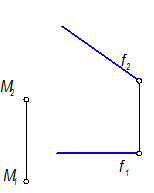
Расстояние между прямыми - это перпендикуляр n(n1, n2).

Начинаем построение с n2, т. к. f || П1, n2 ^ f2 (теорема о проецировании прямого угла).
На чертеже нет натуральной величины n, т. к. n(n1, n2) – прямая общего положения

Определяем | n | методом прямоугольного треугольника.
Просмотрите решенные задачи, назовите номера задач, в которых сразу получается " решающее положение", без дополнительных построений. Алгоритм решения написать самостоятельно (Модуль 4).
|
|
|


