 |
Задача №86. OK = R - прямая общего положения, поэтому на П1 и П2 радиус спроецировался с искажением. Методом прямоугольного треугольника определяем натуральную величину R(ОК) Þ О1К0
|
|
|
|
Задача №86
Построить сферу с центром в точке О, касательную к прямой h.
Если найти точку касания сферы с прямой h(h1, h2) и соединить ее с центром О(О1, О2), то этот отрезок определит радиус R(R1, R2) сферы. Кратчайшее расстояние определяется перпендикуляром, следовательно, проводим R ^ h (R1 ^ h1).

OK = R - прямая общего положения, поэтому на П1 и П2 радиус спроецировался с искажением

Методом прямоугольного треугольника определяем натуральную величину R(ОК) Þ О1К0.

Построить проекции сферы, замерив полученное значение R(О1К0).
Задача №87
Через точку М провести прямую n ^ S(h || k)
Взаимная перпендикулярность прямой и плоскости подробно рассмотрена в Модуле 4, стр. 2, 3, 4.
n ^ S Þ n1 ^ h1; n2 ^ f2

S - плоскость общего положения, но задана двумя параллельными горизонталями, поэтому сразу можно построить через точку М1 Î n1, n1 ^ h1.

В любом месте построить f(f1, f2), принадлежащую плоскости S, затем через М2Î n2 провести n2 ^ f2
Задача №88
Задачу решить самостоятельно, построив сначала h и f Ì S, затем n1 ^ h1, n2 ^ f2
Задача №89
Определить расстояние от точки М до плоскости S(h Ç f).
Как уже отмечалось (М4 -8), это сложные по составу задачи, они решаются в несколько этапов, и на каждом этапе решается отдельная, небольшая конкретная задача.
В данном случае, эта графически сложная задача состоит из трех задач, которые встречались Вам раньше:
1) Из точки М построить n ^ S (задания №87, 88);
2) Найти точку пересечения n Ç S Þ К (первая ГПЗ по 3 алгоритму);
3) S - плоскость общего положения, следовательно, n - прямая общего положения (М4-2, 3).
Методом прямоугольного треугольника найти | n | (задания №82, 85, 86)

Из точки М провести перпендикуляр к плоскости S: т. е. n1 ^ h1; n2 ^ f2
|
|
|
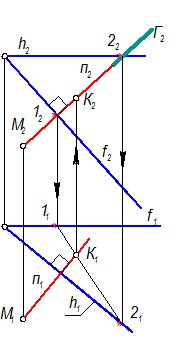
Построить точку пересечения n Ç S Þ К, 1 ГПЗ 3алгоритм.
Г - плоскость посредник, Г ^^ П2, nÉ Г Þ Г2 = n2
Г Ç S = 1, 2 (прямая) 2 ГПЗ 2 алгоритм,
1121 Ç n1 Þ К1, К Î n Þ К2.
МК - искомый отрезок.
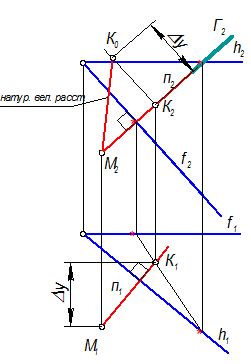
МК - отрезок общего положения. |МК| = М2К0 - натуральная величина.
Задача №90
Определить расстояние от точки М до плоскости S(S2).
Если плоскость S занимает проецирующее положение, то прямая, перпендикулярная ей, является линией уровня (М4-3).

Т. к. S || П2, то n ^ S - фронталь Þ n2 ^ S2; n1 ^ линии связи.

Построить h, f Ì S (задача №27)

Решающее положение для определения расстояния между точкой и плоскостью.
Построить n1 ^ h1, n2 ^ f2
|МК| = М2К2 - натуральная величина расстояния от точки до плоскости.
Задача №91
Построить все множество точек, одинаково удаленных от точек А и В.

Все множество точек, равноудаленных от двух точек (А и В), это плоскость, например, S (DMND), проведенная через середину (точка С Þ АС = СВ) расстояния между ними, S ^ АВ

Соединим точки А и В, разделим пополам графически (циркулем).

Построим через точку С плоскость S(h Ç f), h1 ^ А1В1, f2 ^ A2B2.
Задача №92
Определить расстояние от точки В до прямой а.
В этой задаче нужно построить перпендикуляр к прямой общего положения. (М4 - 4. Взаимная перпендикулярность двух прямых общего положения).
Этапы решения:
1) Из точки В построить S(h Ç f) ^ а (задание №91);
2) Найти точку пересечения а Ç S Þ К (первая ГПЗ по 3 алгоритму) (задание №89);
3) а - прямая общего положения, следовательно, n (ВК) - прямая общего (М4-4) положения. Методом прямоугольного треугольника найти |ВК| (задания №82, 85, 86)
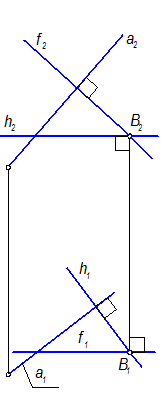
Построим плоскость S(h Ç f) ^ а, причем h1 ^ а1; f2 ^a2.

Решить задачу:
S Ç а = К Þ 1 ГПЗ, 3 алгоритм, см. задачу № 89.
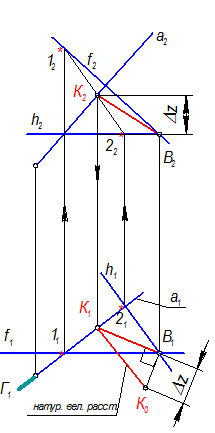
ВК - отрезок общего положения. |ВК| = В1К0 - натуральная величина.
|
|
|


