 |
Задача №93. В плоскости S построить в любом месте фронталь и горизонталь - h,f Ì (а Ç в). Метод введения новой плоскости проекций
|
|
|
|
Задача №93
Через прямую m провести плоскость Г, перпендикулярную заданной плоскости S.
Известно, что две плоскости взаимно перпендикулярны, если в одной из них лежит прямая, перпендикулярная другой плоскости. Таким образом, построение взаимно перпендикулярных плоскостей общего положения сводится к построению взаимно перпендикулярных прямой и плоскости (М4-5).

В плоскости S построить в любом месте фронталь и горизонталь - h, f Ì (а Ç в)
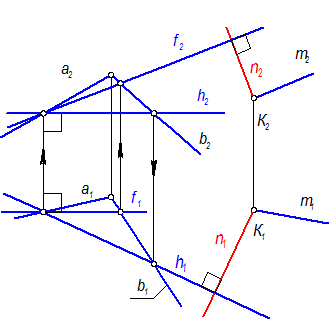
Построить Г ^ S, Г = m Ç n = K. Через точку К провести n ^ S Þ n1 ^ h1, n2 ^ f2.
Задача №95
Построить конус вращения, если S - его вершина, а точка М принадлежит основанию, расположенному в плоскости S.
Чтобы решить задачу, сначала нужно построить ось вращения конуса i(i1i2) перпендикулярно основанию. Но основание принадлежит S, значит i ^ S, но S ^^ П1, то ось i - прямая уровня (См. задание №90), в данном случае - горизонталь. Следовательно i1 ^ S1; i2 ^ линиям связи Þ О1 и О2.

Провести i ^S Þ точка О. Полученное графическое решение соответствует графическому условию задачи №25, поэтому подробности дальнейшего решения не приводятся.

Метод введения новой плоскости проекций
Задача №100
Определить расстояние от точки до прямой.
Вы могли убедиться в графической сложности решения подобной задачи - № 92. Применение способов преобразования комплексного чертежа упрощает решение (М4 -23).
Такое положение оригинала относительно некоторой плоскости проекций, при котором по проекции можно непосредственно определить нужную метрическую характеристику, называется " решающим положением" оригинала.
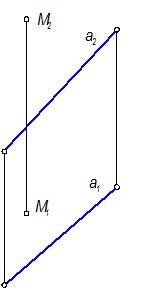
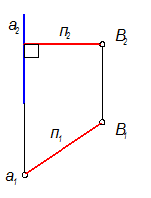
Решающее положение для определения расстояния между точкой и прямой. Горизонтальная проекция n Þ n1 есть искомая величина, т. к. перпендикуляр занимает положение горизонтали в системе П1 - П2.
|
|
|
Прямая а занимает общее положение, чтобы добиться решающего положения, нужно решить первую и вторую задачи преобразования комплексного чертежа.
Решение первой задачи преобразования к. ч.
1) Фиксируем систему П1 –П2 проводим ось Х12
2) П2 Þ П4,
П4 ^ П1, П4 || a Þ x14 || a4
а(а4) - заняла положение прямой уровня в системе П1 – П4, при этом расстояние КМ будет перпендикулярно а (К4М4 ^ а4) Þ n4

Решение второй задачи преобразования к. ч. , т. е. поставить прямую а в системе П4 –П5 в проецирующее положение.
П1 Þ П5
П4 ^ П5, П5 ^ a Þ x45 ^ a4

Закончить решение задачи - это значит построить проекции точки К на П1 и на П2, т. е. сделать возврат от К5 Þ К4 Þ К1 Þ К2. Построить МК (прямая общего положения) в системе П1 – П2.

Задача №101
Определить расстояние между прямыми.

а || в - прямые общего положения.
Чтобы решить задачу, т. е. добиться решающего положения, нужно решить первую и вторую задачу преобразования комплексного чертежа. Подробности см. М4-23 (рис. 4 - 52, 53)
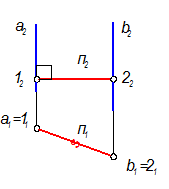
Решающее положение для прямых а и в в системе П1 –П2.
Задача №102
Определить расстояние между прямыми.
c, d - скрещивающиеся прямые, занимают общее положение.
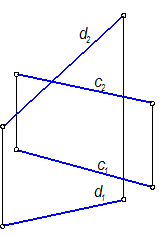
Чтобы решить задачу, т. е. добиться решающего положения, нужно решить первую и вторую задачу преобразования комплексного чертежа, т. е. одну из прямых поставить в проецирующее положение.

Решающее положение для прямых с и d в системе П1 – П2, как в задаче №83
Решение первой задачи преобразования к. ч., чтобы прямая общего положения d заняла положение прямой уровня в системе П1 – П4.
П2 Þ П4
П1 ^ П4, П4 || d Þ x14 || d1

Решение второй задачи преобразования к. ч., т. е. поставить прямую d в системе П -П в проецирующее положение.
П1 Þ П5,
|
|
|
П4 ^ П5, П5 ^ d Þ x45 ^ d4
КМ (К5М5 ^ с5) - натуральная величина расстояния между скрещивающимися прямыми с и d.

Возвращение точек К и М на П1 и П2.
К Ì d, М Ì с, М4К4 ^ d4, т. к. d4 - натуральная величина d, далее КМ строится по линиям связи.

|
|
|


