 |
Задача №103. Определить расстояние от т. М до плоскости (АВС) . Расстояние от точки до плоскости - есть перпендикуляр (МК ^ S)
|
|
|
|
Задача №103
Определить угол наклона плоскости S(а Ç в) к плоскости П2
Такие задачи требуют сложного графического решения, например: задачи № 22, 23, 24. Применение способов преобразования к. ч. значительно упрощает решение. В данной задаче достаточно решить третью задачу преобразования к. ч., заменить П1 Þ П4, т. е. П4 ^ П2, Решающее положение: на П4 плоскость S(S4) вырождается в прямую, угол между х24 Ù S4 = искомый.
Решить самостоятельно.
Задача №104
Определить расстояние от т. М до плоскости (АВС)
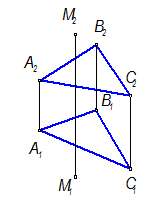
Расстояние от точки до плоскости - есть перпендикуляр (МК ^ S). Чтобы добиться решающего положения, необходимо решить третью задачу преобразования к. ч. (М4-16), при этом отрезок МК займет положение прямой уровня.
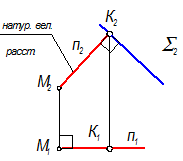
Решающее положение.
Меняем П2 на П4, П4 ^ П1
П4 ^ S; П4 ^ h Þ x14 ^ h
М4К4 ^ S4, MK(M4K4) - натуральная величина расстояния от точки М до плоскости S(АВС).
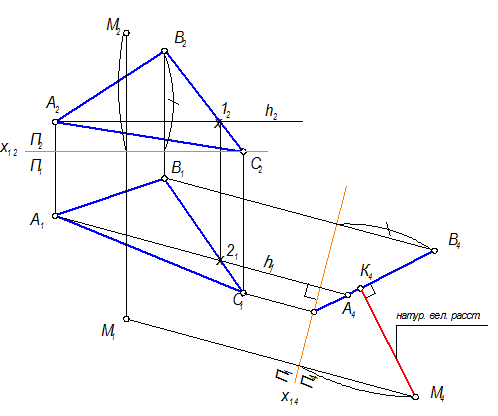
Проводим n1 ^ h1, из точки К4 проводим линию связи до пересечения с n1 Þ К1. К2 находим через П4(как показано на чертеже), можно через построение f(f1, f2) Ì АВС Þ n2 ^ f2.

Возвращение построения К, т. е. отрезка МК в систему П1 Þ П2: К4 Þ К1 Þ К2.
Задача №105
Определить истинную величину двугранного угла.

Если две плоскости, например Ф Ç Г Þ АВ, поворачивать до тех пор, пока они не займут проецирующего положения относительно какой - либо плоскости проекций, то угол между ними спроецируется без искажения, для этого нужно решить первую и вторую задачи преобразования комплексного чертежа.
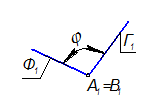
Решающее положение в системе П1- П2
В данной задаче, чтобы обе плоскости оказались одновременно в проецирующем положении, нужно в проецирующее положение поставить прямую АВ.
|
|
|
Решение первой задачи преобразования к. ч. ,
чтобы прямая общего положения АВ заняла положение прямой уровня в системе П1 – П4.
1) Ось х12 проведем через точку В2
2) П2 Þ П4,
П1 ^ П4; П4 || АВ Þ x14 || A1B1
3) Точки С и D переносим на П4 аналогично т. А.

Решение второй задачи преобразования к. ч., т. е. поставить прямую АВ в системе П4 – П5 в проецирующее положение.
П1 Þ П5
П4 ^ П5; П5 ^ AB Þ x45 ^ AB
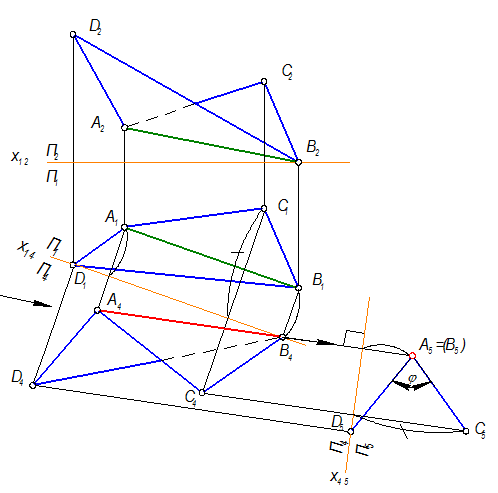
Угол j - истинная величина.
Задача №106
Построить все множество точек, равноудаленных от плоскости S(h Ç f) на 20 мм.
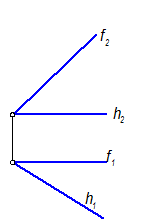
Множеством точек, равноудаленных от плоскости S, будут две плоскости параллельные заданной. Построим только одну плоскость Ф, т. к. другая будет строиться идентично, по другую сторону от S.
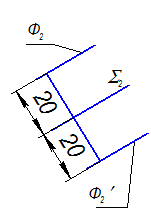
Решающее положение в системе П1 –П2.
П2 Þ П4,
П1 ^ П4; П4 ^ h Þ x14 ^ h1
n4 ^ S4 = 20мм; S4 || Ф4

Для построения плоскости Ф на П1 – П2 достаточно построить:
n1 ^ h1; n2 ^ f2 и вернуть только одну точку 3 в систему П1 – П2
Задать Ф(h, f) || S Þ h1’ || h1, h2’ || h2, f1’ || f1, f2’ || f2

Задача №107
Построить все множество точек, равноудаленных от трех заданных точек.
Все множество точек, равноудаленных от трех заданных, является перпендикуляр, восстановленный в центре описанной, вокруг DАВС, окружности. Центр окружности будут находиться на пересечении проведенных через середины сторон треугольника DАВС перпендикуляров. Решающее положение - истинная величина фигуры DАВС, чтобы добиться такого положения, нужно решить третью и четвертую задачи преобразования к. ч.
Плоскость АВС - общего положения в системе П1 – П4 сделать проецирующей.
1) ось х12 проведем через точку А2
2) Меняем П2 на П4, П4 ^ П1
3) П4 ^ ABC; П4 ^ h Þ x14 ^ h1
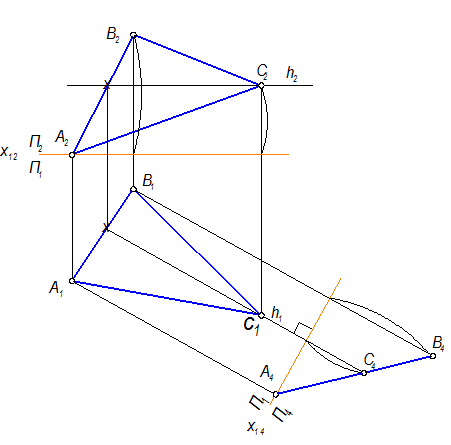
В системе П4 – П5 плоскость АВС станет плоскостью уровня: А5В5С5 - натуральная величина.
Меняем П1 на П5
П5 ^ П4; П5 || ABC Þ x45 || A4B4C4

DА5В5С5 - натуральная величина DАВС. Стороны DАВС Þ А5С5 и С5В5 разделить пополам (точки M5, N5), на пересечении перпендикуляров их этих точек (M5, N5) отметить центр окружности Þ О5, О5 = n5 - проекция искомого перпендикуляра. Сначала построим проекцию перпендикуляра – n4 на П4 в точке О4 Þ по линиям связи, n4 ^ А4В4С4, т. к. плоскость А4В4С4 - проецирующая.
|
|
|
|
|
|


