 |
Задача №107. Через точку О1 проведем n1 ^ h1. Построим f (f1,f2) Ì АВС, проведем n2 ^ f2. На перпендикуляре n4 взять произвольно точку К4 и построить ее по аналогии с точкой О:
|
|
|
|
Задача №107
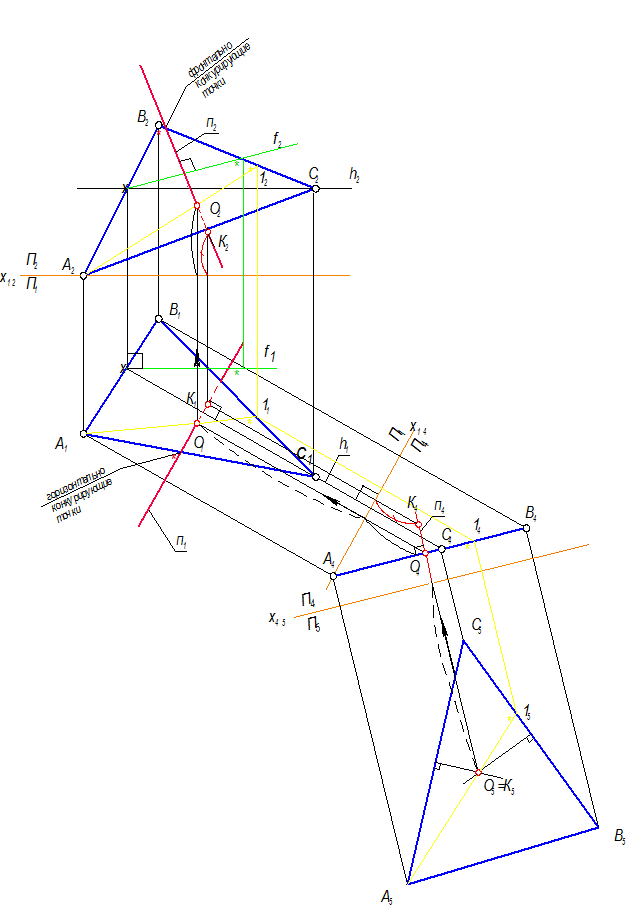
Возвращение перпендикуляра n в систему П1 – П2.
1 - способ:
Вернем точку О по линиям связи на П1 и П2 Þ О1 Þ О2
Х14О1 = Х45О5; Х12О2 = Х14О4.
Через точку О1 проведем n1 ^ h1. Построим f (f1, f2) Ì АВС, проведем n2 ^ f2.
2 - способ:
На перпендикуляре n4 взять произвольно точку К4 и построить ее по аналогии с точкой О:
Х14К1 = Х45К5; Х12К2 = Х14К4.
3-способ:
Точку О в системе П1 – П2 можно построить и через свойство принадлежности точки прямой данной плоскости:
О5 Î А515 Þ А414 Þ А111 Þ А212
С помощью конкурирующих точек определим видимость n1 и n2.
Задача №109
Построить проекции линии пересечения поверхности
конуса с плоскостью (АВС).
= в (плоская кривая) 2ГПЗ, 3 алгоритм, такая задача графически сложна; применяя
способы преобразования к. ч., упрощаем решение. Если плоскость (АВС) поставить в частное
положение, то можно перейти к решению данной задачи по 2 алгоритму.
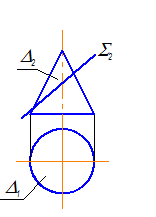
Решающее положение в системе П1 –П2
Ось Х12 проводим через основание конуса. Заменим П2 Þ П4, П4 ^П1
П4 ^ ABC; П4 ^ h Þ x14 ^ h1
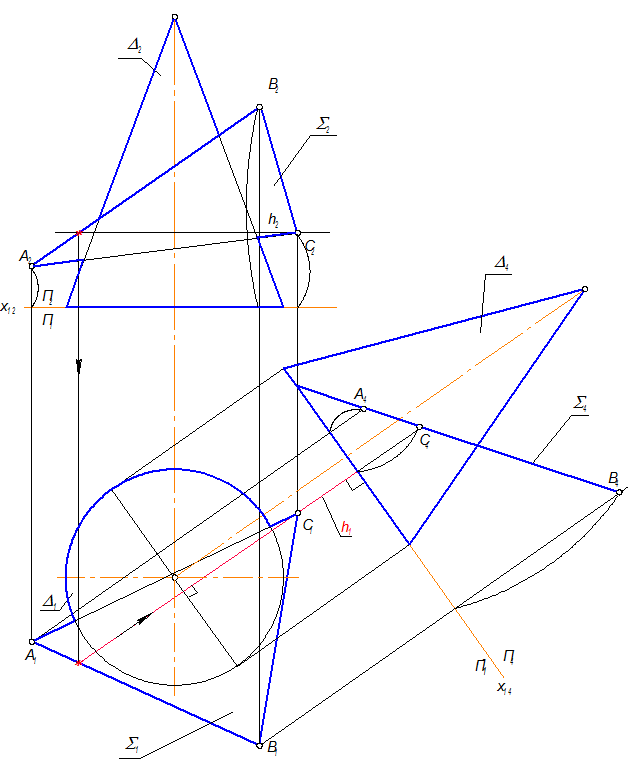
D Ç S = в (плоская кривая) Þ 2ГПЗ, 2 алгоритм.
S4 - для построения достаточно и двух точек, например, А4 и В4.
Способ решения: каждая точка строится сразу на П1 и П2.
Заменим П2 Þ П4, П4 ^ П1
П4 ^ ABC; П4 ^ h Þ x14 ^ h1

Способ решения. Кривая простраивается по точкам сначала на П1 затем на П2
Система координат П4- П1:
D Ç ABC = в (эллипс)
2 ГПЗ, 2 алгоритм
ABC ^^ П4 Þ A4B4C4 = в4
Построить в1 Ì D (см. М-27)

Заключительным этапом будет построение фронтальной проекции кривой в2. Высоту каждой точки (аппликаты) берут на П4 и переносят на П2. Проекцию кривой в вычерчивают с учетом видимости.

Задача №110
Построить проекции линии пересечения поверхности тора с S(h Ç f).
|
|
|
Г Ç S = в (плоская кривая) Þ 2ГПЗ, 3 алгоритм: такая задача графически сложна. Применяя способы преобразования к. ч., упрощаем решение. Если плоскость S(h Ç f) поставить в частное положение, то можно перейти к решению данной задачи по 2 алгоритму.

Решающее положение в системе П1 – П2
1) Ось Х12 проходит через основание тора.
2) Заменим П2 Þ П4, П4 ^ П1
3) П4 ^ S, П4 ^ h Þ x14 ^ h1

Дальше решение продолжить самостоятельно (см. задачу №109), при решении размеры не проставлять.
Метод вращения вокруг проецирующей оси
Задача №115
На поверхности сферы построить точку, наиболее близко расположенную к точке В.
Для решения задачи применим метод вращения вокруг проецирующих осей.

ВО - прямая общего положения, на которой и находится точка А, наиболее близко расположенная к точке В.
1. Прямую ВО повернем так, чтобы она стала прямой уровня.
Ось вращения i ^ П2
|В 1’О1| - натуральная величина.

Задача №116
Вращением вокруг оси i совместить точку А с плоскостью S(h Ç f).

Задача №117
Определить натуральную величину сечения пирамиды плоскостью Г методом вращения вокруг проецирующей оси.
Ось вращения i ^ П2.

|
|
|


