Изучение законов сохранения энергии и импульса при ударе

 

Цель работы

Ознакомиться с явлением удара на примере соударения подвешенных на нитях шаров.

Идея эксперимента

Исследование упругого и неупругого удара шаров позволяет экспериментально проверить законы сохранения импульса и энергии, на базе которых выведены рабочие формулы, а также установить некоторые закономерности ударов. Проводится сопоставление теоретических выводов и экспериментально полученных результатов.

Теория

Удар – совокупность явлений, возникающих при кратковременном приложении к телу внешних сил, связанных со значительным изменении его скорости за очень краткий промежуток времени. Удар обычно протекает в течение тысячных или даже миллионных долей секунды. Удар называется центральным и прямым,если при ударе центры тяжести тел лежат на линии удара, а их относительная скорость параллельна линии удара. В зависимости от упругих свойств тел, характер удара может изменяться от абсолютно упругого до абсолютно неупругого. Рассеивание энергии при ударе, т.е. переход механической энергии в другие виды, характеризуется коэффициентом восстановления скорости k _ск или коэффициентом восстановления энергии k _э.

Коэффициент восстановления скорости определяется как отношение модуля относительной скорости тел после удара к модулю относительной скорости тел до удара

                                                        ,                                                    (5.1)

где v_{1 ,} v₂ – скорости тел до удара, u_1, u₂ – скорости тел после удара.

Коэффициент восстановления энергии определяется как отношение суммарной кинетической энергии тел после удара к суммарной кинетической энергии тел до удара

                                                             .                                                         (5.2)

Нетрудно убедиться, что для абсолютно упругого удара k_э=1 и k _ск =1, а для абсолютно неупругого удара k_ск=0. В реальных ударах 0<k_э<1 и 0< k _ск <1. Величина коэффициентов восстановления зависит от физических свойств материалов соударяющихся тел, от их формы, а для неупругого удара также в сильной степени зависит от масс соударяющихся тел.

В данной работе изучается центральный удар двух шаров, подвешенных на нитях. Опыты будут ставиться так, что один из шаров до удара покоится.

Упругий удар шаров

Обозначим массы шаров m ₁ и m ₂, скорости шаров до удара 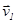  и , скорости шаров после удара и  соответственно. К абсолютно упругому соударению шаров применим как закон сохранения импульса, так и закон сохранения механической энергии

                                                             .                                    (5.3)  

Решение этой системы уравнений позволяет найти скорости шаров после удара

                                            и  ,                            (5.4)

или, разделив числитель и знаменатель этих выражений на m ₁:

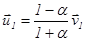                                                  и   ,                              (5.5)

где a = m₂/m₁ – отношение масс шаров.

Величина a всегда положительна, поэтому второй шар после удара всегда движется в ту же сторону, куда двигался первый шар до удара. Первый же шар после удара может продолжать движение в ту же сторону, что и до удара, если его масса больше массы второго шара (a <1), или же отскакивать, если его масса меньше массы второго шара (a >1). В случае равенства масс шаров (a =1), первый шар после удара останавливается, а второй шар, неподвижный до удара, начинает двигаться со скоростью первого шара (обмен скоростей).

Отношение кинетической энергии , переданной во время удара первоначально покоящемуся шару, к кинетической энергии ударяющего шара  определяется соотношением

                                                            .                                     (5.6)                                           

Величину f можно условно назвать эффективностью упругого удара. Она дает долю энергии первого шара, которую получил второй шар после удара. Между величинами f и a существует взаимно однозначное соответствие, в то время как одному и тому же a могут соответствовать множество значений энергии в зависимости от начальных значений скорости 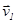. Нужно отметить, что ход f(a) не зависит от начальной скорости  или m₁ и m₂, а только от отношения m₂/m_1. Исследование функции (5.6) показывает, что второй шар получает от первого наибольшую энергию в том случае, когда массы шаров равны, т. е. при a =1. При этом f=1 и , вся энергия достается второму шару, а первый после удара останавливается.

Как уже указывалось, в реальном ударе часть кинетической энергии шаров переходит во внутреннюю энергию, и в предлагаемом случае, когда 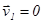, . Поэтому зависимость (5.6) выполняется только с определенной степенью точности.

Неупругий удар шаров

В сущности, любой реальный удар является неупругим. Рассмотрим такой неупругий удар, после которого шары «слипаются» и движутся с одинаковой скоростью 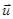. Применяя к этому удару закон сохранения импульса, можно получить выражение для общей скорости  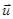шаровпосле удара

                                                 или      ,                      (5.7)

где a - по-прежнему отношение масс шаров.

Коэффициент восстановления энергии при неупругом ударе равен

. (5.8)                                                    

Он оказывается зависимым от отношения масс шаров.

Интересно также вычислить величину, которая показывает, какая часть кинетической энергии соударяющихся шаров преобразуется во внутреннюю энергию. Эту величину можно назвать эффективностью неупругого удара

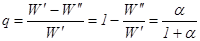,   (5.9)

где и - суммарные энергии системы до и после удара.

Очевидно, что q, рассматриваемая как функция от a, есть неизменная теоретическая функция. В то же время, эта функция, будучи просчитана по результатам измерений энергий и , является экспериментальной и может отличаться от первой.

Предыдущая12345678910111213141516Следующая

Поделиться:

Воспользуйтесь поиском по сайту: