 |
Исследование собственных колебаний струны методом резонанса
|
|
|
|
Цель работы
Произвести наблюдение формы собственных колебаний струны при неизменном ее натяжении и исследовать зависимость скорости распространения поперечной волны в струне от ее характеристик.
Идея эксперимента
В работе собственные колебания струны исследуются методом резонанса. Явление резонанса заключается в следующем: если частота вынуждающей силы, периодической во времени и приложенной к малому участку струны, становится равной одной из собственных частот струны, то в ней устанавливаются стоячие волны с максимальной амплитудой колебаний. При этом необходимо, чтобы участок приложения вынуждающей силы совпадал с одной из пучностей соответствующей стоячей волны. Стоячая волна получается в результате наложения волн одинаковой частоты и амплитуды, распространяющиеся в противоположных направлениях (частный случай интерференции).
Теория
В натянутой между двумя закрепленными точками струне при возбуждении колебаний устанавливаются стоячие волны. Так как точки закрепления струны являются узлами стоячих волн, то в струне возбуждаются колебания лишь таких частот, при которых на длине струны l укладывается целое число полуволн l /2. Отсюда
(11.1)
где l – длина струны.
Учитывая связь скорости распространения колебаний v с частотой n и длиной волны l, получаем для скорости
(11.2)
Скорость распространения волны зависит только от собственных характеристик струны и определяется по формуле
|
|
|
(11.3)
где P, d, r - натяжение, диаметр и плотность материала струны соответственно. Подставляя значения скорости в формулу (11.2), получаем окончательное выражение для собственных частот колебаний струны:
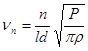(11.4)
Самая низкая собственная частота (или самый низкий тон, издаваемой струной) получаемый при n = 1
(11.5)
называется основной частотой или основным тоном. Более высокие частоты, кратные
n 1, называются обертонами основной частоты или гармониками. Основная частота называется первой гармоникой, удвоенная основная частота или первый обертон – второй гармоникой и т.д.
Приняв за начало координат одну из точек закрепления струны и направив ось х вдоль струны, запишем уравнение n - й стоячей волны:
, (11.6)
где x n – поперечное отклонение точки струны с абсциссой х в момент t, 
– амплитуда, 
. Профиль стоячей волны в любой момент времени имеет форму синусоиды и представляет собой график распределения смещений и амплитуд по оси х. Частоты колебаний всех точек струны одинаковы и определяются по формуле (11.4).
Итак, струна, закрепленная на двух концах, не может находиться в простом гармоническом колебании с любой частотой, допустимы лишь частоты, определяемые формулой (11.4).
В общем случае в струне могут устанавливаться одновременно колебания самых разных частот, но кратных основной частоте, так как струна представляет собой систему с гармоническими обертонами.
|
|
|
Экспериментальная установка
В схеме установки, представленной на рисунке 26, струна из медной проволоки натягивается на некоторой высоте между двумя стойками-струбцинами. Один конец струны закреплен неподвижно, а к другому концу, перкинутому через блок, прикреплена платформа с грузами, с помощью которых в струне создается натяжение.
От генератора электрических колебаний на струну подается регулируемое по частоте переменное напряжение. Вдоль струны может свободно перемещаться постоянный магнит.
Участок струны с текущим по нему переменным током попадает в поле постоянного магнита. При этом возникает периодическая сила, приложенная к струне. Частота изменения этой силы равна частоте переменного тока. В том случае, когда частота генератора будет совпадать с одной из собственных частот струны, а положение полюсов магнита – с пучностью стоячей волны, соответствующей данной частоте, наблюдается явление резонанса: в струне устанавливается стоячая волна.
Проведение эксперимента
Измерения и обработка результатов
1. Между двумя струбцинами, укрепленными на столе, натягивают тонкую медную проволоку. Для обеспечения надежного электрического контакта место закрепления конца струны и место ее касания блока должны быть предварительно хорошо зачищены с помощью наждачной бумаги. На свободный конец струны подвешивают платформу для грузов. К клеммам на струбцинах подключают выход генератора.
2. Включают генератор звуковых частот.
3. Создают натяжение в струне, поместив на платформу для грузов какой-либо разновес. При определении натяжения струны учитывается масса платформы. Для первого опыта рекомендуется взять общую массу груза 120-140 г.
4. С помощью микрометра измеряют диаметр струны, а с помощью линейки ее длину.
5. Устанавливают магнит посередине струны и, плавно изменяя частоту вращением лимба генератора (в районе 20 - 30 Гц), добиваются устойчивых колебаний основного тона. Затем увеличивают частоту колебаний в кратное число раз и, передвигая магнит вдоль струны, получают устойчивые колебания последующих обертонов. Если амплитуды колебаний малы, следует увеличить выходное напряжение на генераторе.
6. Записывают в таблицу 11.1. отчета в порядке возрастания значения частот звукового генератора, при которых на струне устанавливаются стоячие волны. Вычерчивают профили стоячих волн.
|
|
|
7. Подставляют в формулу (11.2) полученные значения резонансных частот и вычисляют скорость волны в струне для различных опытов. Находят среднее значение скорости при данном натяжении струны. Оценивают погрешность измерения скорости. При этом можно использовать результаты первого опыта, очевидно дающий наибольшую погрешность. Погрешность в измерении собственных частот колебаний струны равна половине цены делений на лимбе генератора.
8. Изменяют первоначальное натяжение струны. В результате этого изменяется скорость распространения поперечных волн и набор собственных частот. Проводят измерения и вычисления согласно пп. 5 и 7 при других натяжениях. Рекомендуется варьировать натяжение струны ступенчато через 0,5 Н.
9. По формуле (11.3) рассчитывают теоретические значения скорости волны в струне при различных натяжениях. (Расчеты проводятся в системе СИ; плотность меди r = 8,9 × 103 кг/м3). Оценивают погрешность такого расчета.
10. В выводе сопоставляют измеренные и вычисленные значения скорости.
11. Для проверки характера зависимость скорости волны в струне от величины натяжения строят график зависимости квадратов измеренных скорости распространения от величины ее натяжения.
|
|
|
