Уравнения состояния. Смеси жидкостей, паров и газов. Общие соотношения

Уравнения состояния

При относительно низком давлении и высоких температурах реальные газы имеют малую плотность и, с известным допущением, могут рассматриваться как газы идеальные.

Уравнение состояния идеального газа (Клапейрона (1834 г. ) для G кг и       

для 1 кг соответственно    

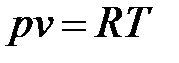   ; ,                                              (1. 21)                                

где  – характеристическая постоянная газа (Дж/(кг× К).

Газовые постоянные для различных тел определяются свойствами рабочих тел и поэтому имеют различные значения. Умножив на молекулярную массу ( 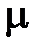) обе части уравнения (1. 21) получим уравнение Клапейрона – Менделеева

       для 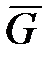=  кмолей газа                                     (1. 22)

или

       для 1 кмоля газа       ,                                 (1. 23)

 

где ( м³/ кмоль) – молярный объем, при нормальных физических условиях (P = 0, 1Мпа и t = 0⁰C) равен 22, 4 м³/ кмоль; Дж/(кмоль× К) – универсальная газовая постоянная.

Отсутствие теоретически обоснованного единого уравнения состояния реального газа привело к выводу большого количества эмпирических и полуэмпирических уравнений состояния, справедливых для отдельных газов в ограниченном диапазоне изменения параметров их состояния.

Наиболее простым, качественно отображающим поведение реальных газов является  уравнение  состояния Ван-дер-Ваальса которое содержит две константы

P + a/v²)(v – b) = RT,                                       (1. 24)

где  a и b –экспериментально полученные константы; a /v² – поправка на силы молекулярного сцепления; b – поправка на объем молекул.

В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента (z), называемого коэффициентом сжимаемости

.                                               (1. 25)

 

Коэффициент сжимаемости (z)учитывает различие между идеальным и реальными газами (для идеального газа z = 1).

Коэффициент сжимаемости является функцией давления, температуры и зависит от природы газа.

Для обобщения данных по коэффициентам сжимаемости различных газов был использован принцип «соответственных» состояний, сформулированный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ.

В критической точке для всех веществ r = 0,

, , .

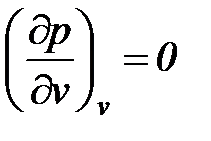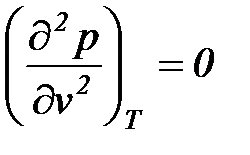Вещества находятся в соответственных состояниях при одинаковом удалении от критической точки.

Степень удаления от критической точки определяется с помощью приведенных параметров:

· приведенного   давления ;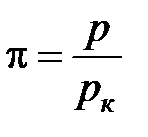

· приведенной   температуры ;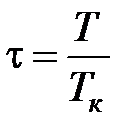

· приведенного объема .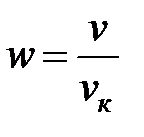

Уравнение состояния, записанное в виде F ( ) = 0, называется приведенным уравнением состояния. Оно не содержит индивидуальных констант вещества.

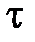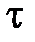Состояния вещества, в которых они имеют одинаковые  и  называются соответственными. Зная параметры  и   определяется коэффициент сжимаемости z.

. Смеси жидкостей, паров и газов

Общие соотношения

Термодинамическая система – объект исследования термодинамики, может представлять собой смесь химически не взаимодействующих между собой чистых веществ. Предполагается также, что структура отдельных компонентов смеси в процессе смесеобразования и стабилизации смеси не изменяется.

Из закона сохранения материи следует, что масса смеси G равна сумме масс составляющих ее компонентов G_i

 

,                                             (1. 187)

 

а число киломолей смеси  равно сумме числа киломолей всех компонентов смеси

 

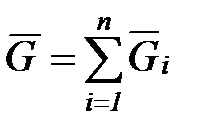,                                           (1. 188)

 

где 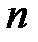 – число компонентов в смеси.

Одной из важнейших характеристик смеси является ее состав. Он задается массовыми или молярными концентрациями (долями) компонентов.

Массовой концентрацией или массовой долей m_i называется отношение массы компонента к массе всей смеси

 

.                                                  (1. 189)

 

Молярной концентрацией или молярной долей i-го компонента 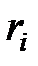 называется отношение количества киломолей этого компонента  к общему числу киломолей смеси

 

.                                             (1. 190)

Очевидно, что для термодинамических смесей справедливы следующие соотношения:

 

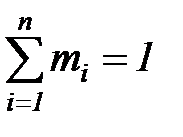, .                                    (1. 191)

 

Средняя (кажущаяся) молярная масса смеси 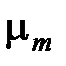 равна отношению массы смеси к количеству киломолей смеси и может быть определена из следующих соотношений:

 

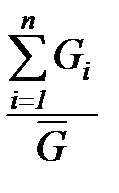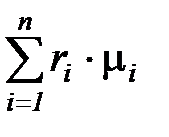 =  =  = ;                    (1. 192)

 

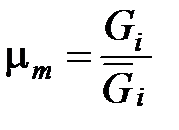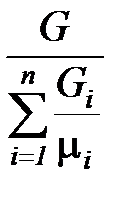 =  =  =  = .                (1. 193)

 

Зависимость между массовой и молярной концентрациями устанавливается соотношением

 

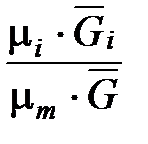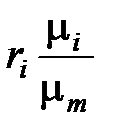 =  =                                  (1. 194)

или

.                                            (1. 195)

 

Газовая постоянная смеси  может быть вычислена по следующему выражению:

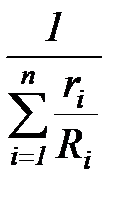 = = ,                           (1. 196)

 

где =8314 Дж/(кмоль К) – универсальная газовая постоянная, R_i – характеристическая газовая постоянная компонента смеси.

Для жидких, твердых и газообразных смесей часто используется и понятие объемной концентрации компонентов. Объемной концентрацией i-го компонента  называется отношение объема данного компонента V_i  к объему всей смеси V

.                                                           (1. 197)

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: