Аналитическое выражение первого начала термодинамики

Аналитическое выражение первого начала термодинамики

Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом:

 

;                                              (12)

 

.                                          (13)

 

Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями

 

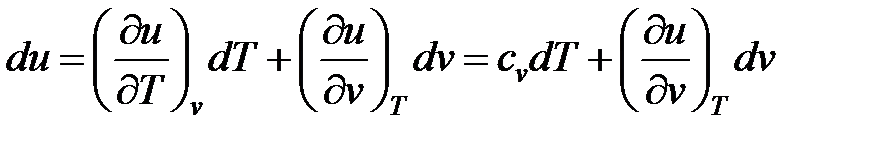;                    (14)

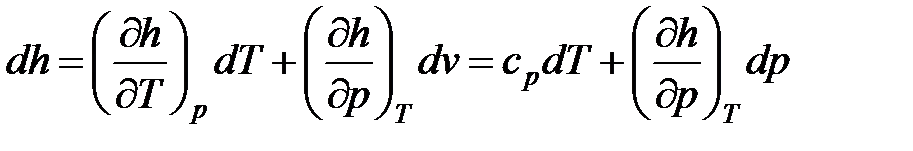.                    (15)

 

    Соотношения (14) и (15) получены, исходя из анализа зависимостей, который показывает, что для изохорного процесса ( ) частная производная внутренней энергии по температуре равна истинной изохорной теплоемкости

 

,                                              (16)

 

а для изобарного процесса ( 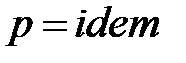) частная производная энтальпии по температуре равна истинной изобарной теплоемкости

 

.                                              (17)

 

В результате подстановки выражений (16) и (17) в уравнения (14, 15) и разделения переменных получим:

 

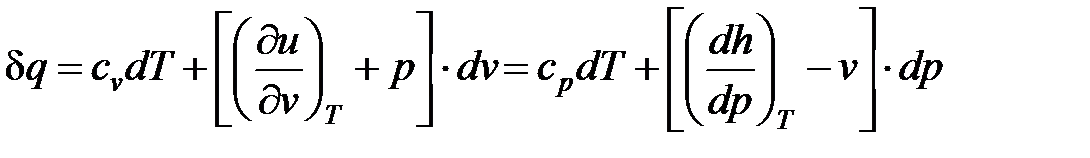.               (18)

 

Выражения в квадратных скобках уравнения (18) в литературе часто называют калорическими коэффициентами, которые могут быть определены по формулам, полученным с использованием дифференциальных соотношений термодинамики,

h_v = ,                      (19)

h_p = 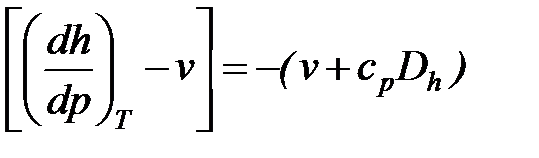,                  (20)

где  – коэффициент Джоуля – Гей Люссака,

 

;                                           (21)

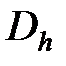 – коэффициент Джоуля-Томсона,

.                                              (22)

Коэффициенты Джоуля – Гей Люссака ( ) и Джоуля-Томсона ( ) реальных газов определяются по таблицам термодинамических свойств, представленным в справочной литературе.

 

Данное соотношение (18) называется первым началом термодинамики для простых тел в аналитической форме.

 

Первое начало термодинамики для идеальных газов.

Закон Майера. Энтропия идеального газа

Идеальные газы подчиняются уравнению состояния Клапейрона 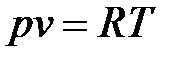 и закону Джоуля, согласно которому удельная внутренняя энергия идеального газа зависит только от температуры

.                                                 (23)

 

Совместное использование уравнения Клапейрона и закона Джоуля приводит к выводу о том, что удельная энтальпия идеального газа также являются функциями только температуры

.                                      (24)

 

С учетом законов идеальных газов и исходя из соотношений (14, 15), изменение внутренней энергии 1 кг идеального газа в элементарном и конечном (1-2) процессах находится по следующим формулам:

 

; ,                            (25)

 

а изменение энтальпии 1 кг идеального газа в элементарном и конечном

 (1-2) процессах определяется по следующим зависимостям:

 

; .                                          (26)

 

После подстановки соотношений (25) и (26) в выражение первого начала термодинамики для простых тел (10, 11) получаем уравнение первого начала термодинамики для идеального газа по балансу рабочего тела в дифференциальной и интегральной формах:

 

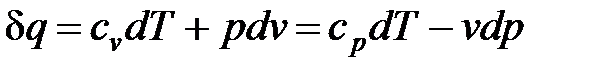;                   (27)

 

. _.                (28)

 

Из уравнения первого начала термодинамики для идеального газа (28) можно получить следующее выражение:

 

,                  (29)

 

из которого следует, что разность истинных теплоемкостей идеального газа при постоянном давлении и при постоянном объеме равна величине характеристической газовой постоянной

 

.                                          (30)

 

Это выражение (30) впервые было получено Р. Майером (1842 г. ) и называется законом Майера.

Уравнение (30) может быть записано и для одного кмоля газа

 

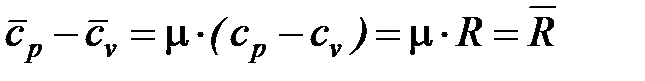.                          (31)

 

Разделив уравнение (27) на абсолютную температуру T, получим

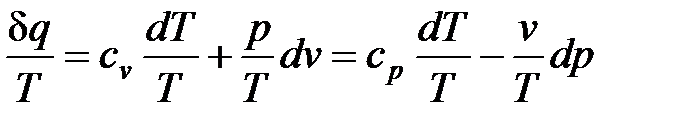.                          (32)

 

С учетом того, что для идеального газа, исходя из уравнения

Клапейрона, справедливы равенства: ;  получим

 

.                  (33)

 

Правая часть уравнения (33) представляет собой сумму полных дифференциалов. Это значит, что и соотношение  есть полный дифференциал некоторой функции состояния идеального газа(s), называемой удельной энтропией.

Изменение удельной энтропии в элементарном процессе представляет собой полный дифференциал и определяется соотношением

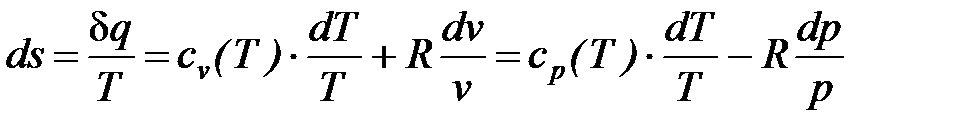      (34)

 

Из уравнения (34) после интегрирования получим, что изменение удельной энтропии идеального газа в процессе (1-2) может быть найдено из соотношения

 

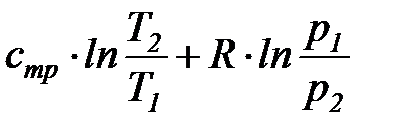 = .             (35)

 

Теплоемкости  и  называются вторыми средними теплоемкостями и находятся путем осреднения по логарифму абсолютных температур

 

.                              (36)

 

Если принять, что истинная теплоемкость является линейной функцией температуры , то

 

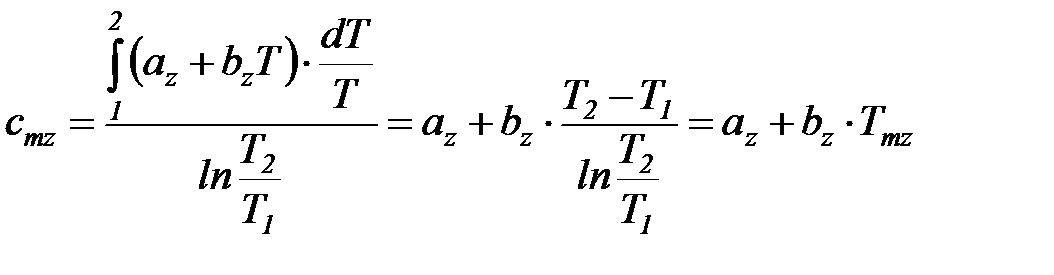.           (37)

 

Таким образом, первая средняя теплоемкость равна истинной теплоемкости при средней арифметической температуре процесса (T_ma ), а вторая – при средней логарифмической температуре процесса (T_mz). В случае, если , то первая средняя теплоемкость численно несколько больше второй.

 

 

Процессы изменения состояния термодинамических систем

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: