Схемы смешения. Смеси идеальных газов

Схемы смешения

При образовании смесей на практике встречаются две основные схемы смешения: при постоянном объеме (V = idem, рис. 1. 20а) и постоянном давлении (p = idem, рис. 1. 20б).

 

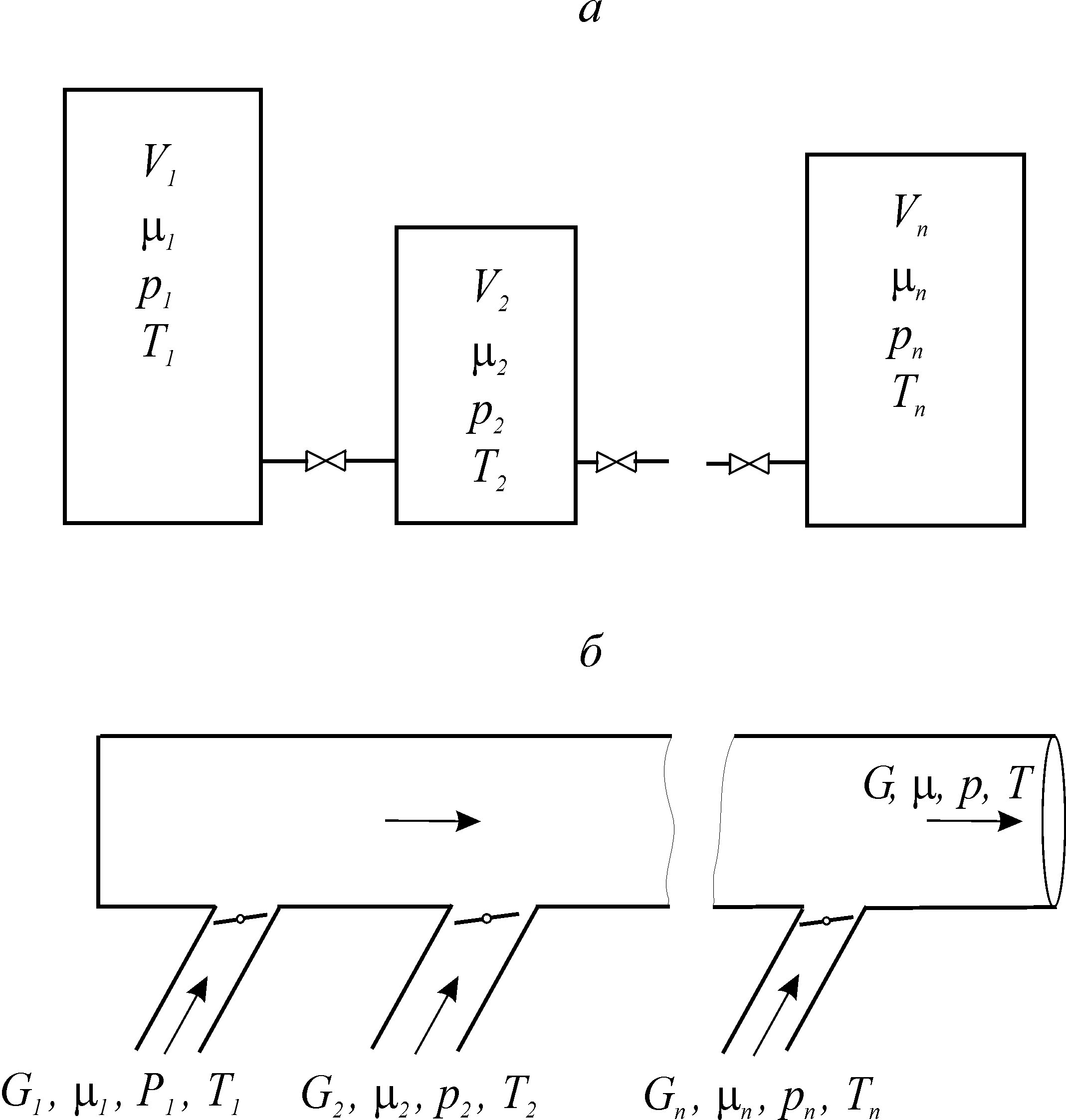
Рис. 1. 20. Схемы смешения при постоянном объеме (а)

и при постоянном давлении (б)

 

При расчете и анализе схемы смешения при постоянном объеме рассматривается система, включающая ряд резервуаров, соединенных трубопроводами с установленными на них кранами (рис. 1. 20а). В каждом резервуаре
объемом V_i находится один компонент с известными исходными
параметрами (G_i,  , ,  T_i ). После открытия кранов во всех резервуарах происходит выравнивание давления p_m, а затем температуры T_m и концентрации компонентов (m_i, r_i) – система переходит в состояние термодинамического равновесия. Во всех стадиях процесса смешения полный объем системы сохраняет неизменную величину V = .

В процессе смешения по схеме с постоянным объемом теплота извне не подводится ( ) и внешняя работа не совершается ( ) и, следовательно, исходя из первого начала термодинамики по внешнему балансу (1. 35), получаем, что этот процесс смешения идет без изменения внутренней энергии

( ).                               (1. 198)

 

Смесеобразование при постоянном давлении происходит в трубопроводах (рис. 1. 20б). К общему трубопроводу отдельными потоками подводятся компоненты. Для каждого компонента известны: массовый расход G_i, молярная масса m_i , давление p_i  и температура T_i . Смесеобразование в трубопроводе возможно лишь в случае, когда давление каждого компонента p_i больше среднего давления смеси в трубопроводе . При прохождении запорного устройства давление компонента уменьшается до среднего давления смеси  – отсюда наименование схемы ( ).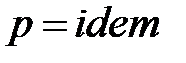

Заключительные стадии процесса смешения при 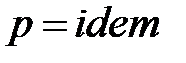 – выравнивание температур, концентраций компонентов в смеси (диффузионные процессы) и переход системы в состояние термодинамического равновесия.

В процессе смешения при 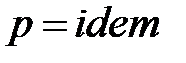 теплота извне не подводится ( ) и внешняя работа не совершается ( 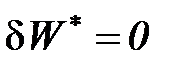) и, следовательно, исходя из первого начала термодинамики по внешнему балансу для потока (81), получаем, что этот процесс смешения идет без изменения энтальпии

 

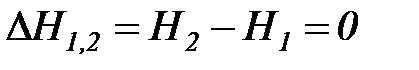( ).                            (1. 199)

 

Смеси идеальных газов

Смеси идеальных газов являются также идеальными газами и подчиняются уравнению состояния идеальных газов (уравнению Клапейрона)

 

,                                 (1. 200)

 

где ,  – давление и температура смеси.

Средняя температура и среднее давление смеси характеризуют конечное состояние диффузионного равновесия смеси.

Состояние компонентов смеси в процессе перемешивания непрерывно изменяется, начиная с момента первичного выравнивания давлений компонентов и кончая состоянием диффузионного равновесия, когда давление каждого из компонентов снижается до уровня стабильного парциального давления .

Закон диффузионного равновесия смеси идеальных газов (закон Дальтона) характеризует установившееся состояние газовой смеси и формулируется следующим образом: каждый компонент смеси ведет себя в газовой смеси так, как будто он один при температуре смеси 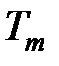 равномерно распространен во всем объеме смеси  и развивает при этом давление, которое называется парциальным .

Уравнения состояния для i-го компонента и всей смеси идеальных газов могут быть представлены в следующем виде:

 

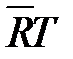 = ;                                                   (1. 201)

 

.                                             (202)

 

При делении уравнения (1. 201) на уравнение (1. 202) получаем

 

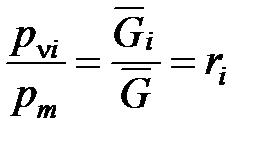.                                           (1. 203)

 

Из соотношения (1. 203) следует, что парциальное давление i-го компонента 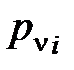 в смеси идеальных газов определяется через полное давление смеси  и молярную концентрацию компонента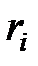

 

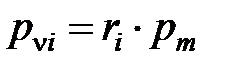.                                           (1. 204)

 

После преобразования соотношения (1. 204) получаем, что сумма парциальных давлений всех компонентов смеси идеальных газов равна полному давлению смеси

 

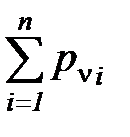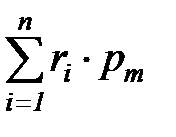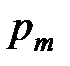 =  =  = .                        (1. 205)

 

Поскольку внутренняя энергия и энтальпия идеального газа - функции только температуры, исходными соотношениями для определения средней температуры смеси идеальных газов  служат следующие соотношения:

в схеме смешения при  

 

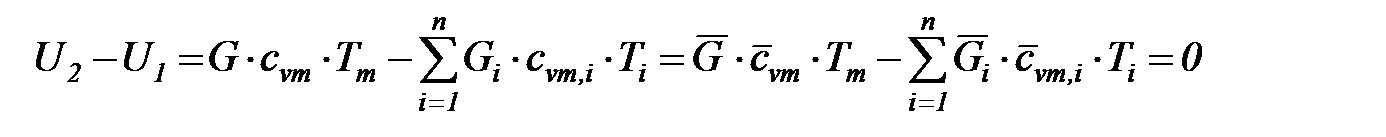; (1. 206)

 

в схеме смешения при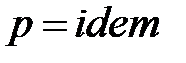  

 

. (1. 207)

 

С учетом этих соотношений (1. 206), (1. 207) получаем обобщенное выражение по определению средней температуры смеси идеальных газов  для различных схем смешения

 

,                     (1. 208)

 

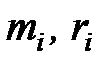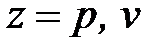где  – массовая и молярная концентрации i-го компонента смеси;  – средние удельные массовая и молярная теплоемкости i-го компонента смеси в процессах  ( );  – средние удельные массовая и молярная теплоемкости смеси,

 

,                                        (1. 209)

 

.                                         (1. 210)

 

Объемная концентрация каждого компонента в смеси  определяется как отношение приведенного объема v_{i, пр} компонента при давлении и температуресмеси к объему всей смеси v при тех же условиях

 

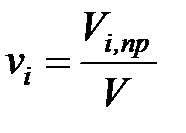.                                                          (1. 211)

 

Для идеального газа, исходя из уравнения состояния

 

v_{i, пр} = , v = .                                (1. 212)

 

После подстановки  v_{i, пр}  и  V  в соотношение (1. 211) получаем

 

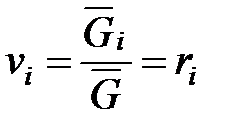.                                              (1. 213)

 

Отсюда следует, что для смесей идеальных газов объемная и молярная концентрации компонентов численно равны.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: