Смеси реальных газов. Первое начало термодинамики

Смеси реальных газов

Для расчетов характеристик смесей реальных газов обычно используется следующее уравнение состояния

 

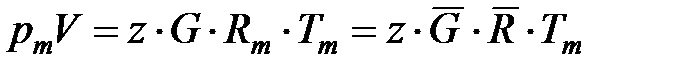.                           (1. 214)

 

Определение значений коэффициента сжимаемости z для реальных газовых смесей проводится с использованием закона соответственных состояний. Однако, в отличие от чистых газов, характеристики соответственных состояний определяются не по фактическим критическим параметрам, а по значениям приведенных критических (псевдокритиеских) давления p_пк и температуры T_пк газовых смесей:

 

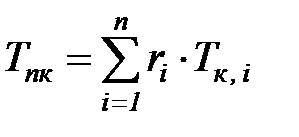; ,                              (1. 215)

 

где  p_{к, i}  и  Т_{к, i} - критические давление и температура компонентов газовой смеси.

Псевдокритические параметры используются для вычисления значений приведенного давлений  p  и температур  t смеси:

 

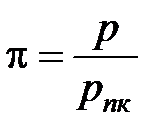; .                                       (1. 216)

 

Первое начало термодинамики

Первое начало термодинамики является математическим выражением закона сохранения и превращения энергии.

Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «внутренняя энергия изолированной системы остается неизменной при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой».

При построении термодинамики принимается, что все возможные энергетические взаимодействия между телами сводятся лишь к передаче теплоты и работы.

В силу того, что теплообмен и передача работы являются единственными формами передачи энергии изменение энергии изолированной системы (т. е. системы, которая энергетический не взаимодействует с окружающей средой или с другой системой) равно нулю du_из=0.

Рассмотрим систему к которой извне подводится или отводится теплота и подводится или отводится термодинамическая работа. В этом случае изменение внутренней энергии системы равно алгебраической сумме подведенных извне теплоты и термодинамической работы (подведенная теплота - положительна, подведенная работа - отрицательна).

 

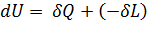,   .              (1)

                                                         

Окончательно исходное выражение первого начала термодинамики формулируется следующим образом: «количество теплоты, подведенное к системе из вне (Q_{1, 2}), идет на изменение внутренней энергии системы и на выполнение работы ( )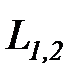

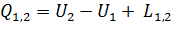                                     (2)

            

В дифференциальной форме уравнение (2, ) может быть представлено следующим образом:

 

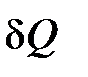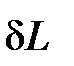=  + .                                                (3)

 

Уравнения (1. ), (2. ), (3) являются математическим выражением первого начала термодинамики справедливое для обратимых процессов и учитывает только внешние эффекты.

Эффективная работа реального процесса 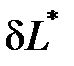 равна разности обратимой работы  и работы необратимых потерь 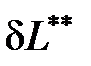 ( 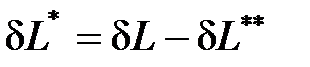). Необратимые потери термодинамической работы ( ) превращается в теплоту внутреннего теплообмена ( ).

Следовательно, в случае реальных процессов, уравнение первого начала термодинамики примет вид

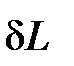
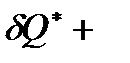
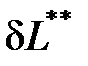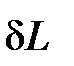=  + или = = =  +            (4а); 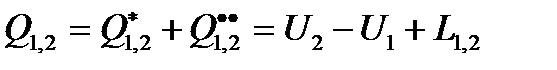,                                           (4б)

Уравнения (4а) и (4б) называются уравнениями первого начала термодинамики по балансу рабочего тела, и они справедливы для реальных процессов.                                             

В обратимых процессах  =  = 0 и уравнения первого начала термодинамики по внешнему балансу и по балансу рабочего тела совпадают.

 

Для простых тел, то есть систем, состояние которых определяется двумя независимыми переменными, математическое выражение первого начала термодинамики в дифференциальной форме имеет следующий вид:

для термодинамической системы

 

;                                (5)

 

для 1 кг системы

 

.                                    (6)

 

Выражение удельной потенциальной работы можно представить в виде соотношения

 

,                      (7)

 

из которого следует, что

 

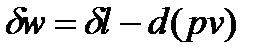; .                            (8)

 

После подстановки выражения (8) в уравнение (6), получим:

 

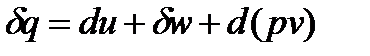, .                   (9)

 

Сумма удельной внутренней энергии ( ) и потенциальной
функции ( 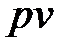) называется удельной энтальпией ( ) (Дж/кг).

Поскольку энтальпия определяется с помощью параметров состояния (u, р, v), то она является функцией состояния и для простого тела может быть представлена в функции любых двух параметров, например, р и Т. Дифференциал функции состояния является полным дифференциалом.

Подобно полной внутренней энергии энтальпия системы является экстенсивным параметром, зависит от количества вещества и определяется по соотношению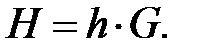  

Математическое выражение первого начала термодинамики для простого тела в дифференциальной и интегральной форме имеет следующий вид:

;                                   (10)

 

.                          (11)

 

Первое начало термодинамики для 1 кг простого тела для реальных систем

( первое начало термодинамики по балансу рабочего тела) в дифференциальной и интегральной форме можно представить в следующем виде:    

 

. (11а)

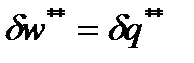.                                            (11б)

 

В обратимых процессах  и поэтому выражение первого начала термодинамики совпадает с выражением первого начала термодинамики по балансу рабочего тела.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: