 |
Тема 3. Меры центральности в графе
|
|
|
|
Из литературы известно, что поиск центрального узла в графе важен, поскольку помогает решить следующие задачи [28]:
1. Быстрое распространение информации в сети.
2. Предотвращение различных эпидемий.
3. Защита сети от распада.
Существуют различные меры центральности (рис. 22):
1. Степень центральности вершины (degree) – характеризует число связей данной вершины с другими вершинами сети. В направленном графе различают входящую и исходящую центральность.
a. Входящая степень центральности (indegree centrality) – число связей, которые входят в данный узел.
b. Исходящая степень центральности (outdegree centrality) – число связей, которые выходят из данного узла.
2. Центральность как посредничество (betweenness).
3. Центральность как близость к другим узлам (closeness). В российской литературе данный показатель называют плотностью центральности.
4. Центральность на основании характеристик соседних вершин (neighbors’ characteristics) – важность, центральность, влиятельность соседних вершин как показатель центральности изучаемой вершины.
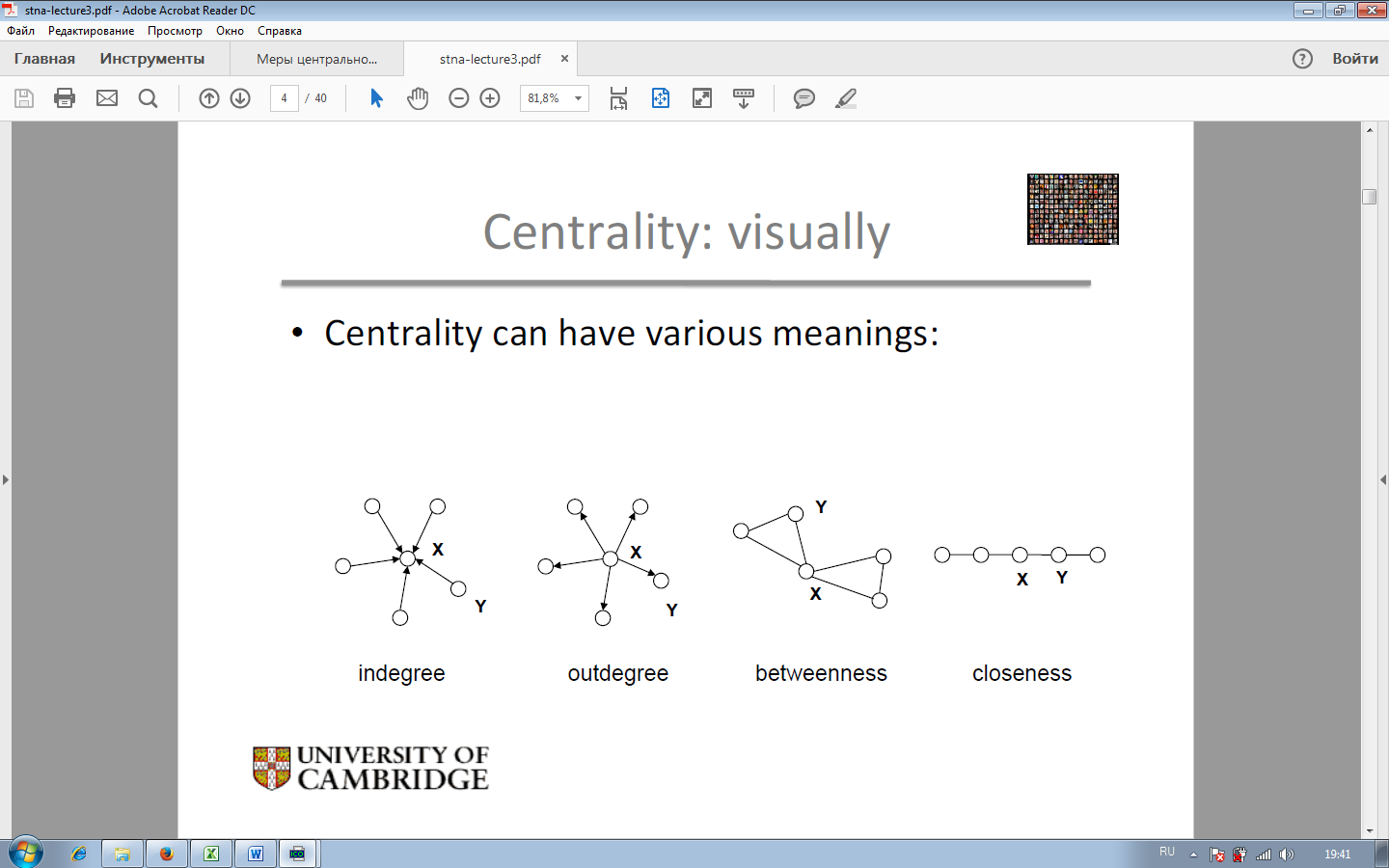
Рис. 22. Основные меры центральности
Каждая мера центральности лучше всего подходит для описания определенной ситуации. Данные характеристики дополняют друг друга. Приведем соответствующие расчетные формулы. Их особенность состоит в том, что они не учитывают направления связей, но, тем не менее, позволяют выявить центральные позиции в сети взаимодействий.
1. Степень (уровень) центральности узла (degree c entrality) – это число связей данного узла с другими узлами. Данную меру центральности лучше всего использовать, когда необходимо определить людей, которые выбирают Вас и с которыми Вы предпочитаете взаимодействовать или, наоборот, от которых держитесь подальше. Формально степень центральности узла можно представить в следующем виде (13) [28]:
|
|
|
, (13)
где 
– степень центральности узла 
;
– связь между вершинами и 
.
Вершина со степенью 
напрямую соединена со всеми другими вершинами, следовательно, она характеризуется высокой степенью центральности (это максимально возможная степень центральности узла).
Чтобы можно было сравнивать степень центральности узла не только внутри одного графа, но и между графами разной структуры, необходимо рассчитать стандартизированную оценку центральности (нормированную центральность узла):
, (14)
где 
– нормированная степень центральности узла ;
– степень центральности узла ;
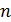– число вершин в сети.
Величина меняется в интервале от 0 до 1 и говорит о том, насколько хорошо вершина напрямую связана со всеми остальными вершинами сети.
Чтобы иметь возможность сравнить различные структуры и определить, какая из них обеспечивает наилучшую централизацию узлов, находят степень центральности всего графа. Она позволяет оценить неоднородность сети и рассчитывается, как отношение суммы отклонений максимальной центральности в сети от центральности каждой вершины к такой же величине в предельном случае. Предельным случаем является сеть, имеющая форму звезды, у которой центральность одной вершины равна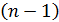 
, а центральность всех остальных 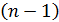вершин равна 1. Сумма отклонений максимальной центральности в сети формы «звезда» от центральности каждой вершины составит 
. Таким образом, степень центральности всего графа находится по формуле Фримана (15).
, (15)
где 
– степень центральности всего графа; 
– максимальная степень центральности узла в сети; – степень центральности узла ; 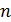– число вершин в сети.
|
|
|
Существуют задачи, с которыми показатель степени центральности справляется хуже, чем другие меры центральности, а именно:
· Оценка посредничества между группами.
· Оценка информированности о происходящих в сети событиях.
2. Центральность как посредничество (betweenness). Центральность узла в этом случае рассматривается как контроль связей между определенными позициями и определяется числом индивидуумов, которые должны будут пройти через данный узел, чтобы достичь другой позиции (16).
, (16)
где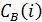 
– центральность как посредничество узла ; 
– число самых коротких путей, соединяющих и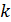 
и проходящих через вершину ; 
– общее количество коротких путей, соединяющих и .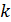
Главную идею данного подхода можно сформулировать следующим образом: узел тем более централен, чем больше количество других узлов, между которыми он находится (чем больше маршрутов он контролирует). Индикатор носит вероятностную интерпретацию. По сути, он показывает долю контролируемых путей. Вероятность того, что связь между и 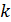пройдет через вершину , равна 
.
Можно рассчитать стандартизированную оценку центральности узла как его посредничества (нормированную центральность как посредничество узла) (17):
, (17)
где 
– нормированная центральность как посредничество узла ; 
– максимальное количество связей между всеми вершинами графа (число пар вершин, за исключением самой вершины).
Центральность как посредничество для группы узлов можно рассчитать по формуле, предложенной Фриманом (18):
, (18)
где 
– степень центральности как посредничества для всего графа; 
– максимальная степень центральности как посредничества для узла в сети; 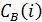– степень центральности как посредничества для узла ; 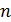– число вершин в сети.
Стандартизированную оценку центральности как посредничества для всего графа можно рассчитать по следующей формуле, предложенной Фриманом (19) [27]:
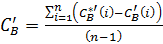, (19)
где 
– нормированная степень центральности как посредничества для всего графа; 
– нормированная максимальная степень центральности как посредничества для узла в сети; – нормированная степень центральности как посредничества для узла ; 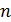– число вершин в сети.
|
|
|
Если для нас не важно наличие большого количества друзей или посредничество между другими людьми, но желательно быть в гуще событий, недалеко от центра, то стоит обратить внимание на такой показатель, как плотность центральности, или центральность как близость к другим узлам.
3. Плотность центральности (closeness) позволяет определить, насколько близко узел располагается относительно других узлов. Если позиция центральна, то узел может быстро взаимодействовать с другими узлами. Данная позиция очень выигрышна при осуществлении коммуникаций. При таком подходе централь – это позиция, из которой необходимо делать минимальное количество шагов ко всем остальным позициям группы. Центральность узла как его близость к другим узлам измеряется следующим образом (20):
, (20)
где 
– плотность центральности узла ; 
– расстояние между вершинами и .
Нормированный коэффициент плотности центральности узла рассчитывается по формуле (21).
, (21)
где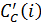 
– нормированная плотность центральности узла ; – плотность центральности узла ; 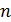– число вершин в сети.
Нормированную плотность центральности группы узлов рассчитывают по формуле (22).
, (22)
где 
– нормированная плотность центральности группы узлов; 
– максимальное нормализованное значение плотности центральности узла ; 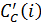– нормированная плотность центральности узла ; 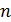– число вершин в сети.
Плотность центральности учитывает число самых коротких путей, но нас может интересовать число всех возможных путей. Так определяется центральность Катца.
4. Центральность Катца рассчитывается по формуле (23).
, (23)
где 
– фактор внимания; 
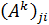– показывает, соединены ли вершины и с помощью 
дуги.
Центральной в ряде случаев может быть названа вершина, связанная с влиятельными вершинами. Ее позицию позволяет определить центральность на основе собственного вектора.
|
|
|
5. Измерение центральности на основе собственного вектора (e igenvector c entrality) осуществляется по формуле (24).
, (24)
где 
– матрица смежности графа;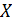 
– собственный вектор (мера центральности); 
– собственное число.
Оценить центральность вершин с учетом их весов позволяет также мера, предложенная Бонасичем.
6. Центральность Бонасича рассчитывается по формуле (25) [29].
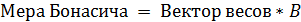, (25)
где 
; E – единичная матрица; – матрица смежности графа; 
; где – собственное число.
Вопросы и задания для самоконтроля
1. Какова роль мер центральности в решении практических задач?
2. Перечислите и охарактеризуйте меры центральности.
|
|
|
