 |
Функции полезности и их виды
|
|
|
|
Предпочтения потребителя могут быть описаны с помощью связанной с отношениями предпочтения функции полезности. Функция полезности или функция благосостояния – функция, с помощью которой можно представить предпочтения на некотором множестве альтернатив. Это выражение зависимости общего уровня полезности набора благ (u) от объема потребления различных благ (qi), входящих в данный набор: 
. С её помощью можно использовать инструментарий теории оптимизации при решении задачи потребителя. Без использования функции полезности решение такой задачи с математической точки зрения может быть затруднительным. С другой стороны, не каждое предпочтение может быть представлено с помощью функции полезности. Тем не менее, несмотря на некоторую ограниченность подхода, функция полезности является неотъемлемой частью большинства современных экономических моделей.
Функция полезности каждому потребительскому набору ставит в соответствие определенное число (полезность) так, что лучшему набору присваивается большее число, а наборам, находящихся в отношении безразличия – то же число. Кривые безразличия отношения предпочтения являются линиями уровня функции полезности.
Формальное определение полезности состоит в следующем.Пусть дано некоторое множество альтернатив 
, на котором определено отношение предпочтения 
. Тогда вещественнозначная функция 
называется функцией полезности, если выполнено условие
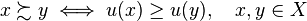
В микроэкономике господствует ординалистский подход к моделированию поведения и выбора. В соответствии с ним числовые значения функции полезности не играют роли, важны лишь соотношения между ними. Если значение функции полезности для одной из альтернатив выше, то эта альтернатива является более предпочтительной для агента. При этом разность значений или частное от их деления не несёт никакой информации. В порядковом подходе полезность товарных наборов определяется с точностью до монотонного преобразования, сохораняющего исходный порядок ранжирования наборов. Свойства предпочтений при порядковом подходе (полная упорядоченность, сравнимость, транзитивность, рефлексивность, ненасыщенность, независимость) интерпретируются как свойства порядковой функции полезности.
|
|
|
При количественном подходе числовые значения полезности имеют существенное значение. Такой подход используется, например, при моделировании поведения агента в условиях неопределенности с использованием функции ожидаемой полезности Неймана-Моргенштерна. В этом случае часто используются денежные, а не абстрактные единицы полезности, и поэтому разность значений имеет экономический смысл.
Условия существования функции полезности:
1) для того чтобы предпочтения можно было представить в виде функции полезности необходимо, чтобы само предпочтение было рациональным, то есть отвечало аксиомам полноты и транзитивности;
2) достаточные условия зависят от самого множества альтернатив и от свойств предпочтений. Если множество конечно или счетно, а отношение предпочтения рационально, то существует функция полезности, которая представляет эти предпочтения;
3) если множество несчетно, то необходима аксиома непрерывности предпочтений, система которых должна быть неоклассической. Достаточные условия существования функции полезности дает теорема Дебрэ, согласно которой, если неоклассические предпочтения непрерывны, то существует непрерывная функция полезности, представляющая эти предпочтения;
4) часто на предпочтения накладываются дополнительные условия, чтобы получить функции с теми или иными свойствами – монотонности, локальной ненасыщаемости и выпуклости.
|
|
|
Непрерывность хотя и является достаточным условием существования функции полезности, представляющей рациональное предпочтение, но оно не является необходимым. Так, например, функция полезности 
(целая часть числа) представляет предпочтения, которые не являются непрерывными. Сама функция при этом также разрывна.
Свойства функции полезности:
1) возрастание потребления одного блага при постоянном потреблении другого блага введет к росту потребительской оценки, т.е. если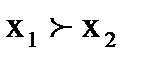 
, то 
и если 
, то 
и наоборот;
2) первые частные производные по каждому аргументу (предельные полезности продукта) положительны: 
; из свойства 2 следует свойство 1;
3) предельная полезность каждого продукта уменьшается, если объём его потребления растёт (закон убывающей предельной полезности);
4) вторые частные производные по каждому аргументу отрицательны: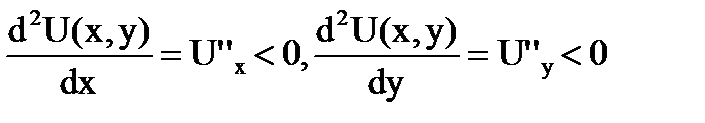 
; из свойства 4 следует свойство 3;
5) предельная полезность каждого блага увеличивается, если растет количество другого блага. В этом случае благо, количество которого фиксировано, оказывается относительно дефицитным. Поэтому дополнительная его единица приобретает большую ценность и может быть потреблена более эффективно. Данное свойство не столь очевидно как 1 или 3, и справедливо не для всех благ: если блага могут полностью замещать, друг друга в потреблении свойства 5 не выполняется (предположение 5 вводится не всегда, но оно гарантирует выпуклость вниз линии безразличия).
Виды функций полезности
1. Функция полезности с постоянным замещением или CES-функция (CES – constant elasticity of substituion) означат постоянную эластичность замещения альтернатив. Функция имеет следующий вид для двумерного случая:
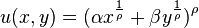
При разных значениях параметра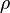 
можно получить частные случаи этой функции (п.п. 2-4).
2. Если 
, то получается линейная функция полезности, которая описывает совершенные заменители (субституты):
В этом случае предельная норма замещения товаров постоянна и равна отношению параметров α и β, которые в свою очередь являются значениями предельных полезностей: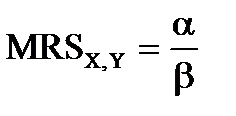 
. Очевидное свойство этих предпочтений – гомотетичность.
|
|
|
3. Если 
, то получается функция полезности Леонтьева, которая описывает совершенные дополнители. Предельная норма замещения в этом случае бесконечна:
Параметры α и β – величины, обратные долям товаров X и Y в потребляемом товарном наборе. В этом случае пропорция потребления задаётся лучом αx = βy. MRSX,Y бесконечна для вертикальных ветвей кривых безразличия, равна нулю для их горизонтальных ветвей и неопределима для вершин, лежащих на указанном луче. Такие предпочтения также гомотетичны.
4. При ρ → 0 получается функция полезности Кобба-Дугласа, если при этом накладывается дополнительное условие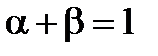 
:
5. Квазилинейная функция полезности:
При квазилинейных предпочтениях каждая кривая безразличия – это вертикально смещённый вариант единственной кривой безразличия. Уравнение для отдельной кривой безразличия: y = k – v(x), где k – различная для каждой кривой безразличия константа. Функция линейна по y, но возможно нелинейна по x.
Все указанные выше функции полезности являются прямыми. В микроэкономической теории потребления также выделяют и косвенную функцию полезности.
Косвенная функция полезности отражает максимальную полезность потребителя в зависимости от цен 
и от дохода 
.
Косвенная функции полезности представляется в виде возрастающей функции дохода и убывающей функцией цен на потребленные товары и услуги. Она отличается от нормальной или прямой функции полезности, где полезность является возрастающей функцией потребленных товаров и услуг. Функция называется косвенной, потому что обычно потребители рассматривают и оценивают наборы в зависимости от количества потреблённых товаров, а не от их цен. Косвенная функция полезности 
может быть вычислена из обычной функции полезности 
через решение задачи максимизации полезности, откуда будет найден наиболее предпочитаемый набор 
(обычный или т. н. маршалловский спрос), тогда косвенная функция полезности будет равна 
.
Свойства косвенной функции полезности:
1) не возрастает по ценам, так как увеличение цен не может сделать доступным тот набор, который соответствует большей полезности;
|
|
|
2) не убывает по доходу, так как при возрастании дохода, как минимум, возможно потреблять прежний набор;
3) однородна нулевой степени по ценам и доходу: если цены и доход возрастут пропорционально на одну и ту же величину («идеальная» инфляция), функция не изменится;
4) прямо пропорциональна относительно доходу и обратно – относительно цен (квазивыпуклая), т. е. может быть записана как линейная функция богатства;
5) частная производная от косвенной функции полезности по цене любого товара равна произведению потребленного количества на предельную полезность дохода;
6) непрерывна во всех внутренних точках (в силу теоремы о максимуме).
|
|
|
