Свойства бюджетного множества

В первую очередь бюджетные множества предполагаются непустыми. В случае бюджетного множества 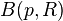для этого достаточно, чтобы доход был больше минимально необходимого для приобретения хотя бы одного допустимого набора, то есть . В случае бюджетного множества это условие означает лишь то, что начальный вектор принадлежит допустимому множеству , что изначально предполагается.

Бюджетное множество является замкнутым, ограниченным и выпуклым. Для ограниченности формально необходимо (и достаточно), чтобы вектор цен был строго больше нуля (то есть все цены должны быть положительными). Замкнутость и ограниченность бюджетного множества обеспечивают существование решения задачи потребителя.

Бюджетное множество 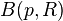является «однородным нулевой степени», то есть если цены и доход умножить на одно и то же число, то получим то же бюджетное множество. В случае бюджетного множества это означает «однородность нулевой степени» по вектору цен.

При фиксированном векторе цен бюджетное множество с меньшим доходом является подмножеством бюджетного множества с большим доходом. При фиксированном доходе бюджетное множество с большими ценами является подмножеством бюджетного множества с меньшими ценами.

Бюджетное множество используется в прямой (маршаллианской) задаче потребителя, заключающейся в максимизации функии полезности на бюджетном множестве альтернатив :

Если задано отношение строгого предпочтения, то задача потребителя сводится к тому, чтобы найти набор из бюджетного множества, такой что любой другой допустимый набор, лучше (в смысле этого отношения предпочтения) данного, не принадлежал к бюджетному множеству.

Прямая задача потребителя

Пусть – функция полезности потребителя, где – вектор альтернатив (потребительских наборов), являющийся элементом допустимого множества . Пусть также – вектор цен, а – располагаемый доход потребителя. Прямая задача потребителя заключается в максимизации полезности на допустимом бюджетном множестве, задаваемом бюджетным ограничением по доходу :

Решением этой задачи является маршалловский (маршаллианский) спрос. Так как функция полезности непрерывна, а бюджетное множество ограниченно и замкнуто (свойство компактности), такая задача всегда имеет решение.

Маршалловский спрос – количество товара, который потребитель приобретет при заданных ценах и доходе, решая задачу максимизации полезности. Иногда он также называется вальрасовским спросом.

Его математическая запись выглядит следующим образом:

где I – доход агента;

– функция полезности;

p – цена;

– маршалловский спрос.

Если непрерывна, доход и цены положительны, то можно доказать, что решение задачи существует. При этом функция 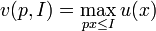является косвенной функцией полезности.

Свойства маршалловского спроса:

1) положительная однородность нулевой степени относительно цен и дохода: ;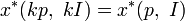

2) для случая локально ненасыщаемых предпочтений подтверждается гипотеза полного расходования потребительского бюджета ();

3) если предпочтения выпуклые, то маршалловский спрос – выпуклая функция; если предпочтения строго выпуклые, то решение задачи максимизации полезности единственно, т. е. является функцией маршалловского спроса;

4) выполняются свойства матрицы Слуцкого (матрицы коэффициентов замещения благ).

Если косвенная функция полезности дифференцируема в точке 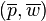, маршалловский спрос может быть вычислен через тождество Роя – отношение предельной полезности по цене и по доходу:

.

Тождество Роя в теории потребления представляет собой связь функции спроса (маршалловский спрос) и косвенной функцией полезности.