 |
Уравнение Слуцкого в анализе потребления
|
|
|
|
Как уже упоминалось выше, 3-ей теоремой теории потребительского выбора является уравнение (тождество) Слуцкого, которое является следствием леммы Шепарда и используется для расчета эффекта дохода и эффекта замещения при изменении цены.
Математически уравнение Слуцкого выводится из дифференцирования маршалловского спроса на i -й товар по цене j -го товара с использованием того факта, что маршалловский спрос выражается через компенсированный спрос при заданных уровнях цен, дохода и полезности.
Смысл тождества Слуцкого – изменение спроса на некоторый товар при изменении его цены складывается из влияния непосредственного изменения спроса и косвенного влияния в результате переключения спроса на другие товары. Данное уравнение показывает, что изменение в спросе на i-й товар при изменении цены j-го товара является результатом двух эффектов – замещения и дохода, а общее изменение спроса равно сумме этих эффектов. Оно выводится следующим образом.
Пусть общее изменение спроса DX есть изменение спроса, вызываемое изменением его цены при сохранении дохода постоянным. Это изменение включает на два изменения – эффект замещения DXС и эффект дохода DXI:
| () |
DX = DXС + DXI.
Здесь тождество Слуцкого записано в абсолютных изменениях, т.е. фиксирует значения эффектов при изменении цены, но не показывает количественной зависимости между изменениями. Поэтому более распространенной является его запись в отношениях изменений. Для этого удобно определить эффект дохода, взятый с обратным знаком: DXI = x(p’,I’) – x(p’,I) = -DXI, подобно тому, что рост цены подобен сокращению дохода, которое в случае нормального товара означает сокращение спроса.
|
|
|
Тождество Слуцкого приобретает вид DX = DXС – DXI. Разделив каждую его сторону на DPX получаем 
.
Уменьшаемое в правой части этого выражения показывает, насколько изменилась величина спроса при изменении цены и такой корректировке дохода, которая позволяет сохранить доступность старого набора, иными словами, показывает эффект замещения. Вычитаемое можно преобразовать с помощью формулы изменения реального дохода: DI = X∙DPХ, отсюда DPX = DI/X. Теперь подставим это выражение в вычитаемое тождества и получим уравнение Слуцкого в относительных изменениях:
| () |
,
Если предположить, что изменения цены незначительны (∆P→0, т.е. ∆I→0), можно записать уравнение Слуцкого в дифференциальной форме:
| () |
,
где 
– общий эффект изменения цены (изменения величины некомпенсированного спроса Маршалла при изменении цены) – показывает, насколько изменилась величина спроса при изменении цены;
– эффект замещения (изменение величины компенсированного спроса Хикса при изменении цены) – показывает, насколько изменилась величина спроса при изменении цены и при фиксированном реальном доходе;
– эффект дохода – показывает, насколько изменилась величина спроса при неизменных ценах (при изменении реального дохода);
Х – объем потребления товара Х.
Если для разграничения эффектов дохода и замещения используется подход Слуцкого, то при исчислении компонента доход фиксируется на уровне, позволяющем при новых ценах приобрести первоначальный набор благ, если подход Хикса – то приобрести набор с прежней полезностью.
Сам эффект дохода в свою очередь состоит из двух сомножителей: изменения величины спроса с изменением дохода (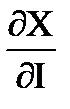
) и первоначального объема спроса (Х).
Общий эффект может быть положительным или отрицательным. В случае нормального товара эффект замещения и эффект дохода действуют в одном и том же направлении. Рост цены означает, что спрос сократится вследствие действия эффекта замещения. Рост цены подобен сокращению дохода, которое в случае нормального товара означает сокращение спроса. Оба эффекта усиливают друг друга.
|
|
|
Влияние, которое изменение цены товара Y оказывает на спрос по товару Х, называется перекрестным эффектом измерения цены. Его также можно разделить на две составляющие: перекрестный эффект замещения и перекрестный эффект дохода. Уравнение Слуцкого для перекрестных эффектов имеет вид:
| () |
,
где 
– перекрестный эффект изменения цены;
– перекрестный эффект замещения;
– перекрестный эффект дохода;
Y – объем потребления товара Y.
Перекрестный эффект замещения всегда действует в том же направлении, в котором меняется цена товара; направление действия перекрестного эффекта дохода зависит от категории товара. По благам низшей категории он действует в том же направлении, что и перекрестный эффект замещения, по нормальным благам – в направлении, противоположном изменению цены.
Если спрос на товар Х изменяется в том же направлении, что и цена товара Y (
), то данная пара благ характеризуется как общие субституты, если наоборот (
), товары – общие комплементы, при 
товары X и Y характеризуются как независимые товары.
Перекрестный эффект цены асимметричен, т.е. реакция спроса по товару Х на изменение цены товара Y может быть сильнее или слабее, чем реакция спроса по товару Y на изменение цены товара Х (
). Также перекрестные эффекты цен по товарам X и Y могут воздействовать на спрос в противоположных направлениях (например, при 
, и наоборот). Вследствие этого сложно отнести товары к конкретной категории.
Чтобы устранить данную асимметрию, необходимо элиминировать влияние перекрестного эффекта дохода, т.е. рассмотреть только перекрестный эффект замещения. Если этот эффект действует в одном направлении с изменением цены (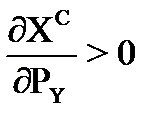
), тогда товары X и Y характеризуются как чистые субституты, если в направлении, противоположном изменению цены (
), товары X и Y – чистые комплементы.
Перекрестный эффект замещения симметричен. Изменение компенсированного спроса на товар Х относительно изменения цены товара Y равно изменению компенсированного спроса на товар Y относительно изменения цены товара Х, т.е. 
. И чем выше перекрестный эффект замещения по абсолютной величине, тем выше степень взаимозаменяемости товаров.
|
|
|
Таким образом, уравнение Слуцкого позволяет:
1) анализировать изменение спроса, описываемого функциями Хикса, не зная самих функций;
2) отнести рассматриваемые товары к той или иной категории в зависимости от направления и величины изменения спроса на них при изменении цен и дохода;
3) если записать это уравнение в терминах коэффициентов эластичностей, то можно оценивать эластичность спроса по Хиксу, используя для этого функции спроса Маршалла.
Подобно тому, как изменения цены воздействуют на спрос через эффекты замещения и дохода, соответственно, коэффициент спроса по цене частично отражает влияние эффекта замещения, частично – эффекта дохода. Для разграничения этого влияния приведем уравнение Слуцкого в коэффициентах эластичности:
| () |
где εp – ценовая эластичность маршаллианского спроса на товар Х;
εcp – ценовая эластичность спроса по Хиксу (компенсированного) на товар Х;
εI – эластичность маршаллианского спроса на товар Х по доходу;
SX – доля расходов на товар Х в доходе потребителя.
Компонент SX∙εI отражает влияние эффекта дохода на ценовую эластичность спроса, компонент εcp – влияние эффекта замещения (коэффициент эластичности замещения, показывающий, как изменяется компенсированный спрос при изменении цены).
Так как значение перекрестной эластичности не дает точного представления о степени взаимозаменяемости товаров, для ее правильной оценки необходимо элиминировать влияние перекрестного эффекта дохода с помощью уравнения Слуцкого для перекрестных эффектов в коэффициентах эластичности:
| () |
где εX,Y – эластичность маршаллианского спроса на товар X по цене товара Y (перекрестная эластичность спроса);
εcX,Y – перекрестная эластичность спроса по Хиксу (компенсированного) на товар X по цене товара Y;
|
|
|
εI,X – эластичность маршаллианского спроса на товар X по доходу;
SY – доля расходов на товар Y в доходе потребителя.
Компонент SY∙εI,X отражает влияние эффекта перекрестного эффекта дохода на перекрестную эластичность спроса, компонент εcX,Y отражает влияние на нее перекрестного эффекта замещения. Коэффициент перекресной эластичности компенсированного спроса 
показывает, как изменится спроса на товар Х под влиянием перекрестного эффекта замещения при изменении цены товара Y. Если 
, товары X и Y характеризуются как чистые субституты, если наоборот – как чистые комплементы; чем больше этот коэффициент по модулю, тем выше степень сопряженности этих товаров.
Оба уравнения Слуцкого в коэффициентах эластичности показывает, что эластичность маршаллианского спроса отличается от эластичности хиксианского спроса на величину эластичности маршаллианского спроса по доходу с учетом доли расходов на товар (или другой товар) в наборе.
|
|
|
