 |
«современные теоретические основы обработки металлов давлением»
|
|
|
|
«СОВРЕМЕННЫЕ ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОБРАБОТКИ МЕТАЛЛОВ ДАВЛЕНИЕМ»
1. Интенсивность внутренних сил. Метод сечений.
Под действием внешних сил в теле возникают внутренние силы, уравновешивающие внешние. Величины внешних и внутренних сил характеризуются их распределением или интенсивностью, т. е. величиной усилия, приходящегося на единицу площадки поверхности на которую она действует. Интенсивность внутренних сил называется напряжением.
Воспользуемся методом сечений. Выделим в деформируемом теле материальную точку, бесконечно малый параллелепипед. Заменим действие отброшенных частей силами. Фрагмент сечения, бесконечно малая площадка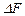 
, на которой действует бесконечно малая сила 
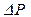, рис. 3. 1.
Рисунок 3. 1 - Напряжение на произвольной площадке
Среднее напряжение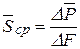 
. Если существует предел этого отношения 
, то утверждают, что напряжение в данной точке существует. Напряжение 
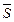представляет собой вектор с направлением действующей силы. Если вектор 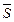по отношению к площадке расположен произвольно, то по правилу параллелепипеда его можно разложить на три составляющие. Одна направлена по нормали к площадке 
и называется нормальным напряжением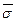 
, две другие взаимно-перпендикулярные, в плоскости площадки называются касательными напряжения 
и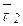 
.
Полное напряжение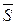 
в точке может быть разложено по правилу параллелепипеда на составляющие, которые расположены не на одной грани, а на взаимно перпендикулярных площадках. При этом грани элементарного объема перпендикулярны этим составляющим, тогда 
.
Если составляющие направлены произвольно относительно граней объема, то последние могут быть разложены тоже по правилу параллелограмма, как это сделано выше, рис. 3. 2.
|
|
|
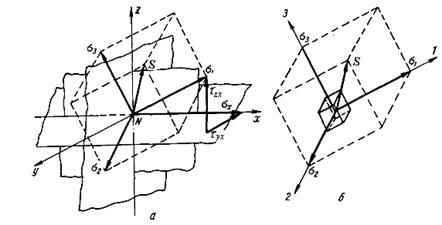
Рисунок 3. 2 - Составляющие полного напряжения
В этом случае векторная сумма:
.
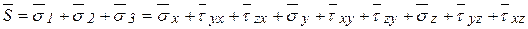Каждая тройка напряжений действует на одной площадке, т. е.:
; 
; 
.
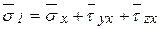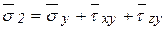Касательные напряжения равны нулю, тогда 
; 
; 
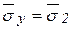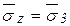, т. е. нормальные напряжения достигают экстремального значения. Направление оси 
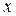определяется единичным вектором 
, оси 
- вектором 
, оси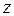 
- вектором 
.
Таблица вида:
= 
,
представляет собой геометрическую сумму указанных векторов, что определяет полное напряжение 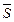. Через единичные вектора можно записать сумму:
.
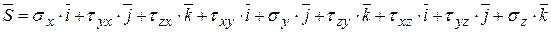Направления площадок, на которых отсутствуют касательные напряжения, задаются единичными векторами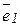 
, 
, 
. Тогда:
.
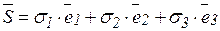Величины, стоящие перед единичными векторами называются проекциями полного вектора напряжений на соответствующую ось. Известно, что проекции вектора определяют этот вектор и по модулю и по направлению. Действительно:
; 
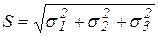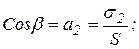
, где 
- углы между вектором полного напряжения и осями 1, 2, 3. При известных направляющих косинусах, определяется направление вектора 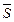в пространстве. Это относится и к произвольным координатам 
. Направления 1, 2, 3 называют главными направлениями.
2. Тензор напряжений. Закон парности касательных напряжений.
Выше показано, используя метод сечений и представление материальной точки в виде элементарного параллелепипеда, вектор напряжения имеет либо три вектора разложения, либо девять векторов разложения полного напряжения 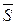, рис. 3. 3
Рисунок 3. 3 - Схема действия напряжений на элементарный объем
Запишем проекции полного напряжения в произвольных координатах в виде таблицы:
- направление 
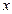
- направление 
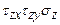- направление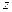 
X Y Z 
Большие буквы X, Y, Z – показывают адреса площадок, нормали которых совпадают с направлениями . Нижние индексы имеют определенное функциональное назначение. Первый индекс показывает направление действия вектора напряжения, второй индекс указывает адрес площадки. Если первый индекс 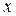, следовательно, напряжение направлено параллельно оси 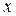. Если второй индекс , следовательно, площадка действия напряжения перпендикулярна оси , а ее нормаль параллельна этой оси. Два одинаковых нижних индекса заменяется одним.
|
|
|
Совокупность девяти величин называется тензором второго ранга. В общем случае тензор характеризует вектор в многомерном пространстве. В соответствии с характеристикой вектора он должен быть задан своими проекциями и по величине и по направлению. Величина напряжения характеризуется совокупностью всех проекций и определяется последовательным применением теоремы Пифагора, а направление - направляющими косинусами, или же направляющим тензором. Вектор в трехмерном пространстве представляется тремя составляющими (проекциями) и называется тензором первого ранга. Скалярная величина – это тензор нулевого ранга. Тензор второго ранга или тензор напряжений:
.
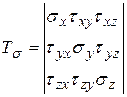Если элементарный объем находится в равновесии, то следует закон парности касательных напряжений, т. е.:
,
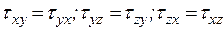касательные напряжения с одинаковыми нижними индексами равны.
С учетом последних соотношений, тензор напряжений записывается
.
Тензор напряжений полностью характеризует напряженное состояние в точке.
|
|
|
