 |
8. Напряжения диагональных площадок.
|
|
|
|
8. Напряжения диагональных площадок.
См. 6-7
Площадки, на которых действуют главные касательные напряжения, ещё называют, диагональными.
9. Шаровой тензор, девиатор напряжений.
Из выражений для определения главных касательных напряжений видно, что с уменьшением или увеличением главных нормальных напряжений на одну и ту же величину значения главных касательных напряжений не изменяются. Это даёт возможность представить тензор напряжений в виде суммы двух тензоров. Введём в рассмотрение среднее нормальное напряжение 
:
.
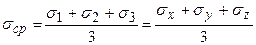Среднее нормальное напряжение равно одной трети линейного инварианта напряжений. Составим шаровой тензор:
.
Вычитаем его из тензора напряжений:
Или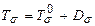 
. Тензор 
называется девиатором напряжений.
Шаровой тензор может представлять равномерное сжатие или растяжение, не влияя на изменение формы. Возможно лишь изменение объёма.
Если напряженное состояние определяется девиатором, то тело изменяет форму без изменения объёма.
10. Октаэдрические напряжения.
Выше были рассмотрены площадки, в которых напряжения и нормальные и касательные принимают экстремальные значения. Это главные и диагональные площадки.
Определим напряжение в площадках, одинаково наклоненных к главным осям. В этом случае 
. Из соотношения находим положение площадки в пространстве:
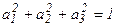, откуда 
.
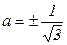Такие площадки образуют фигуру октаэдр. Их называют октаэдрическими, так же напряжения, которые действуют в этих площадках.
Подставляя значение направляющего косинуса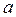 
в выражение для нормального напряжения 
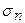, получим нормальное октаэдрическое напряжение:
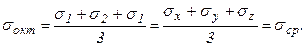
Касательное октаэдрическое напряжение определяется выражением
|
|
|
.
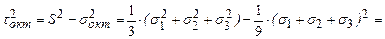
Откуда:
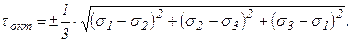
Через главные касательные напряжения:
Для дальнейшего анализа воспользуемся линейным инвариантом тензора напряжений 
в главных напряжениях. Возведем его в квадрат:
квадратный инвариант в главных напряжениях:
.
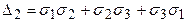Тогда можно записать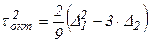 
. Подставляя инварианты в произвольных координатах, получим:
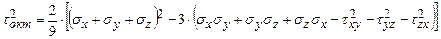
После преобразований:
Квадратный инвариант:
Можно записать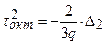 
. Октаэдрические касательные напряжения, второй инвариант являются обобщенной характеристикой напряженного состояния точки, т. к. они определяются всеми составляющими тензора напряжений. Вводится в рассмотрение интенсивность касательных напряжений, которая разными авторами представляется либо как октаэдрическое касательное напряжение, либо, как второй инвариант напряжений. В последнем случае:
Интенсивность касательных напряжений отличается от октаэдрического касательного напряжения тем, что 
есть величина скалярная.
От интенсивности касательных напряжений следует отличать интенсивность напряжений или обобщенное напряжение:
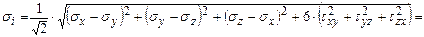
Интенсивность напряжений позволяет формально обобщить некоторые соотношения теории упругости и пластичности при объемном и линейном напряженном состояниях. Например 
, 
. Обобщенный показатель 
характеризует напряженное состояние одним числом, как и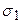 
.
11. Обобщенные характеристики напряженного состояния точки.
См. 10
12. Дифференциальные уравнения равновесия объемного напряженного состояния точки.
Математические модели процессов, явлений описываются дифференциальными уравнениями, которые выводятся из фундаментальных законов природы. В механике на основе условий равновесия или движения.
Напряжения являются непрерывными функциями координат. Выделим в напряженном теле элементарный параллелепипед, рис. 3. 6. Напряженное состояние в точке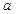 
определяется тензором напряжений:
|
|
|
.
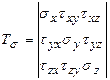Напряжения в точке 
отличается от напряжений в точке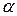 
на бесконечно малую величину. В общем случае для нормального напряжения вдоль оси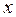 
.
Рисунок 3. 6 - Равновесие элементарного параллелепипеда
Однако если нет смещения точек относительно оси координат 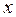, то можно записать 
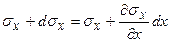. Последнее утверждение позволяет упростить решение задачи. Отсюда тензор напряжений:
.
Условие равновесия элементарного объема определяется уравнениями равновесия.
Алгебраические суммы проекций всех сил на оси координат должны быть равны нулю, т. е.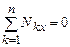 
, 
, 
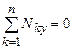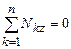. Составляя уравнение равновесия сил на ось 
имеем:
.
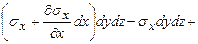
Раскрывая скобки и сокращая на 
, получим:
.
Аналогично уравнения равновесия на оси 
и 
. В итоге:
;
;
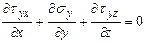Представленные выражения определяют собой дифференциальные уравнения в частных производных и являются условиями равновесия для объемного напряженного состояния. Эти условия обязательны для всех точек деформируемого тела.
Если на тело действуют массовые силы и пластическая деформация испытывает динамическое воздействие, тогда уравнения движения среды:
;
;
.
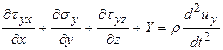где 
- массовые силы, действующие на элементарный объем;
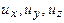- перемещения частиц среды вдоль осей координат 
.
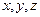Напряжения меняются по объему тела, и в элементах, выходящих на поверхность. Их величина должна быть такой, чтобы уравновесить внешнюю нагрузку, т. е. удовлетворить условиям на контуре.
Частным случаем объемного напряженного состояния является осесимметричное напряженное состояние. Оно относится к телам вращения. Внешние нагрузки расположены симметрично относительно оси и одинаковы во всех меридиональных сечениях. Это осадка цилиндрической заготовки, прошивка, прессование, волочение и т. д. В этом случае используют цилиндрическую систему координат ( 
). Напряжения в цилиндрических координатах, рис. 3. 7.
Тензор напряжений:
.
При осесимметричном напряженном состоянии компоненты напряжений не зависят от координаты 
. В плоскости . не возникает касательных напряжений, вследствие симметрии тела и нагрузок, поэтому:
.
Следовательно, 
будет главным напряжением. Тензор напряжений при осесимметричном напряженном состоянии:
|
|
|
.
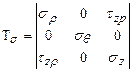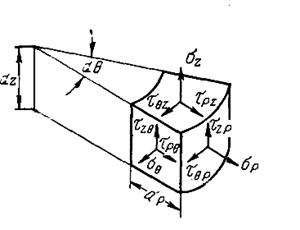
Рисунок 3. 7 - Напряжения в цилиндрических координатах
Принимая тот же метод сечений, запишем условие равновесия сил на оси 
и 
, принимая при этом 
, тогда:
.
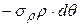
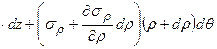
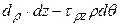
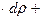
Аналогично проектируя на ось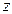 
и, после несложных преобразований и сокращений, получим:
; 
.
При решении некоторых задач касательные напряжения могут отсутствовать. В этом случае вместо двух уравнений равновесия остается одно:
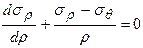
Нормальные напряжения здесь являются главными.
Плоская задача теории пластичности, декартовая система координат. Плоское напряженное состояние или плоско деформированное. Касательные напряжения с нижним индексом координаты, вдоль которой отсутствует компонент напряжения или деформации, равны нулю. Например, 
и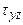 
, тогда:
; 
.
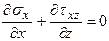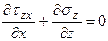В полярных координатах, уравнения равновесия плоской задачи:
;
Возвращаясь к объемному напряженному состоянию для цилиндрических координат можно записать:
;
;
.
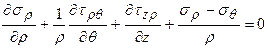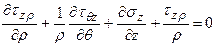Из сопоставления видно, что вид дифференциальных уравнений равновесия зависит от выбранных систем координат.
|
|
|
