 |
3. Общая схема определения напряжений по заданному направлению.
|
|
|
|
3. Общая схема определения напряжений по заданному направлению.
См. 4
4. Нормальные и касательные напряжения наклонной площадки.
Напряжения на наклонной площадке
Составляющие тензора напряжений, исходя из геометрических соотношений, определяют напряжение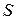 
(напряженное состояние) в данной точке и по модулю и по направлению. Однако этого может оказаться недостаточным, если необходимо определить напряжение по заданному направлению, т. е. на наклонной площадке. Докажем, если заданы напряжения в трёх взаимно перпендикулярных площадках, проходящих через заданную точку, то напряженное состояние по любому направлению будет известно, следовательно будет известным и наряженное состояние в точке.
Проведём через данную точку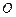 
, рис. 3. 4, плоскость наклона к осям координат. Фигура тетраэдр, сливающаяся с точкой 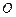. Нормаль 
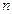перпендикуляра к наклонной плоскости. Ее площадь 
, площади остальных граней 
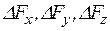. На взаимно перпендикулярные грани действуют составляющие тензора напряжений.
На наклонной грани действует полное напряжение 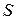. Напряжение может быть разложено по разным направлениям. В данном случае 
.
Если тетраэдр находится в равновесии, то имеем условия равновесия по координатным осям всех действующих сил:
;
;
.
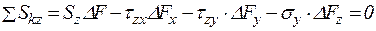Из построения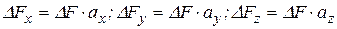 
,
где 
направляющие косинусы
; 
; 
.
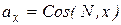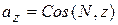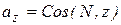Рисунок 3. 4 - Напряжения на наклонной площадке
После преобразований и сокращений на , имеем:
;
;
.
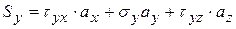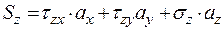Проекции полного напряжения 
на наклонной площадке содержат все компоненты тензора напряжений. По правилу параллелепипеда полное напряжение:
,
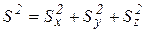направляющие косинусы:
; 
; 
.
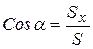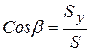Если известны проекции вектора на координатные оси 
, 
, 
, можно определить этот вектор по величине и направлению. В теории упругости и пластичности удобно вектор напряжений разложить не только по координатным направлениям , , , но и по другим, связанных с направлением наклонной площадки. Это нормальное и касательное направление к площадке. Используя теорему о проекции суммы, получим нормальное напряжение к наклонной площадке:
|
|
|
.
Подставляя значения :
Полное касательное напряжение в наклонной площадке по теореме Пифагора:
.
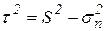По формулам можно определить напряжения в любой наклонной площадке. Если заданы шесть напряжений, действующих в точке по трём взаимно перпендикулярным, то её напряженное состояние определено.
Следует добавить, что выражения могут быть использованы для вычисления внешней силы. Это уравнения связи между внешними силами на контакте и компонентами тензора напряжений или внутренними силами. Ещё их называют условиями на контуре, которые должны входить в математическую постановку задачи теории упругости или пластичности.
5. Экстремальные значения составляющих тензора напряжений.
Касательные напряжения равны нулю, тогда 
; 
; 
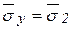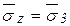, т. е. нормальные напряжения достигают экстремального значения. Направление оси 
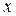определяется единичным вектором 
, оси 
- вектором 
, оси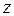 
- вектором 
.
Из рис. 3. 2 видно, что существуют площадки, на которых составляющие тензора напряжений принимают экстремальные значения. Нормальное напряжение – максимальное, а касательное – минимальное, равное нулю. Полное напряжение и нормальное для данных площадок совпадает по величине и направлению. Такие площадки называются главными. Оси, перпендикулярные к главным площадкам называются главными осями, а нормальное напряжение на главных площадках – главными нормальными напряжениями и обозначаются 
. В дальнейшем принимается, что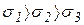 
. Тензор напряжений
.
|
|
|
|
|
|
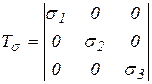