 |
6. Главные напряжения, инварианты напряжений.
|
|
|
|
6. Главные напряжения, инварианты напряжений.
Из рис. 3. 2 видно, что существуют площадки, на которых составляющие тензора напряжений принимают экстремальные значения. Нормальное напряжение – максимальное, а касательное – минимальное, равное нулю. Полное напряжение и нормальное для данных площадок совпадает по величине и направлению. Такие площадки называются главными. Оси, перпендикулярные к главным площадкам называются главными осями, а нормальное напряжение на главных площадках – главными нормальными напряжениями и обозначаются  . В дальнейшем принимается, что
. В дальнейшем принимается, что 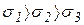 . Тензор напряжений
. Тензор напряжений
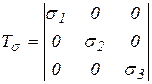 .
.
Рассмотрим наклонную площадку, сориентированной таким образом относительно координатных площадок  ,
,  ,
,  , чтобы полное и нормальное напряжение совпадали, следовательно, площадка была главной.
, чтобы полное и нормальное напряжение совпадали, следовательно, площадка была главной.
Проектируя главные напряжения на оси  ,
,  ,
,  , получим:
, получим:
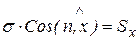 ;
;  ;
; 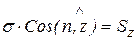 .
.
Подставляя значения 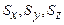 , имеем:
, имеем:
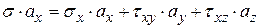 ;
;
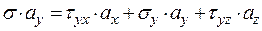 ;
;
 .
.
Или:
 ;
;
 ;
;
 .
.
Кроме этого 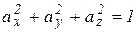 . Последние выражения содержат четыре неизвестных (главное напряжение и его направляющие косинусы). Так, как выражения однородны, кроме этого одновременно косинусы не равны нулю, отсюда определитель системы равен нулю
. Последние выражения содержат четыре неизвестных (главное напряжение и его направляющие косинусы). Так, как выражения однородны, кроме этого одновременно косинусы не равны нулю, отсюда определитель системы равен нулю
 ,
,
где 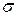 - неизвестная величина главного напряжения.
- неизвестная величина главного напряжения.
Раскрывая определитель, получаем кубическое уравнение вида:
 ,
,
где  - коэффициенты, составленные из компонентов тензора напряжений.
- коэффициенты, составленные из компонентов тензора напряжений.
Так как выбор произвольных площадок определяется поворотом координатных осей, а полное напряжение от этих поворотов не зависит. При этом от поворотов осей не зависят и главные напряжения, которые при векторном суммировании дают полное напряжение. Следовательно, от выбора системы координат не зависят и коэффициенты, являющиеся инвариантами тензора напряжений. При решении кубического уравнения получим три корня. Исследование направляющих косинусов показывают, что главные площадки по отношению друг к другу являются взаимно перпендикулярными. Выражения инвариантов имеют вид – линейный инвариант:
|
|
|
 ,
,
квадратный инвариант:
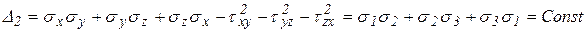 кубический инвариант:
кубический инвариант:
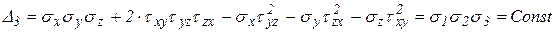
Инварианты напряжений позволяют в дальнейшем определить обобщенные показатели напряженного состояния в главных и произвольных координатах.
7. Общая схема определения главных касательных напряжений.
При заданных величинах главных нормальных напряжений 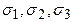 величины напряжений на наклонной площадке
величины напряжений на наклонной площадке 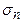 и
и  изменяются при изменении направляющих косинусов нормали к площадке
изменяются при изменении направляющих косинусов нормали к площадке  , т. е. при изменении положения наклонной площадки к главным осям. Касательное напряжение на наклонной площадке:
, т. е. при изменении положения наклонной площадки к главным осям. Касательное напряжение на наклонной площадке:
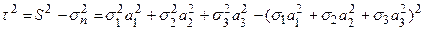 ,
,
 .
.
Выясним, в каких площадках касательные напряжения получают экстремальные значения. Пусть 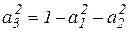 , тогда:
, тогда:
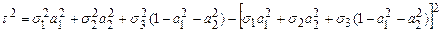 .
.
Дифференцируем по  и приравниваем частную производную нулю, для нахождения экстремума
и приравниваем частную производную нулю, для нахождения экстремума
Преобразуя, имеем

 ,
,
или
 .
.
Дифференцируя уравнение для 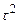 по
по  и приравнивая производную нулю, получим:
и приравнивая производную нулю, получим:
 .
.
Решениями последних уравнений является 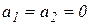 , тогда
, тогда  , которые определяют экстремальные значения
, которые определяют экстремальные значения 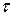 .
.
Далее, приняв  , получим
, получим 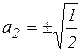 и
и  . Подставляя
. Подставляя 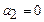 , получим
, получим  .
.
Из условия 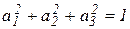 выражаем
выражаем 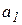 и
и 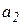 , подставляя их в (
, подставляя их в (  ), и производим, аналогичные выкладки. Получаем шесть групп значений направляющих косинусов, при которых касательные напряжения получают экстремальные значения.
), и производим, аналогичные выкладки. Получаем шесть групп значений направляющих косинусов, при которых касательные напряжения получают экстремальные значения.
Первые три группы значений направляющих косинусов определяют плоскости, в которых касательные напряжения принимают минимальные значения, равные нулю. Вторые три группы значений определяют плоскости, в которых касательные напряжения достигают максимальных значений.
Таким образом, имеем три пары площадок, расположенных под углом 45о к главным, в которых касательные напряжения достигают максимальных абсолютных значений.
|
|
|
Подставляя в выражение для определения касательного напряжения значения направляющих косинусов, определим значения максимальных касательных напряжений:
 ,
, 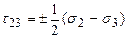 ,
, 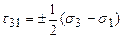 .
.
Эти напряжения называются главными касательными напряжениями.
Нормальные напряжения в этих площадках получаться при подстановке значений направляющих косинусов в выражение для нормального напряжения на наклонной площадке т. е.:
 ,
,  ,
, 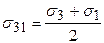 .
.
Площадки, на которых действуют главные касательные напряжения, ещё называют, диагональными.
|
|
|


