 |
15. Уравнения Коши, тензор деформаций.
|
|
|
|
15. Уравнения Коши, тензор деформаций.
См. 14
16. Главные деформации, инварианты деформированного состояния точки.
Выражая длину отрезка через произвольные координаты до деформации и после деформации, преобразуя, имеем следующее выражение для удлинения 
по произвольному направлению:
Удлинение отрезка, проходящего через данную точку, можно выразить через шесть компонентов тензора деформации той же точки. Данное выражение подобно выражению для нормального напряжения по произвольной площадке, проходящей через ту же точку. Двойки множители исчезают, т. к. в тензоре деформации углы приведены с коэффициентом 0, 5.
Между теориями напряжений и деформаций существует полная аналогия. Формулы теории деформаций выражаются аналогично теории напряжений.
Выше показано, существуют направления, которые определяют площадки, где отсутствуют касательные перемещения, отсутствуют сдвиговые деформации. Тензор деформаций:
.
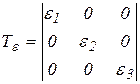Направления этих площадок называются главными осями деформации. Линейные деформации достигают экстремального значения и называются главными. При этом 
. Кубическое уравнение для определения главных деформаций аналогично кубическому уравнению для определения главных напряжений:
,
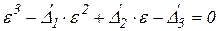где
,
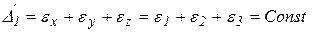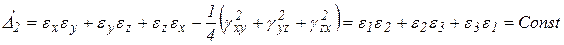
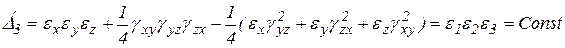
В изотропном теле направления главных напряжений и главных деформаций должны совпадать.
Удлинения и сдвиги в октаэдрических плоскостях запишутся по аналогии с октаэдрическими напряжениями:
,
.
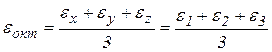В теории пластичности используют величину пропорциональную октаэдрическому сдвигу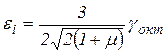 
, которая носит название интенсивность деформации, где 
- коэффициент Пуассона. Для случая одноосного растяжения или сжатия величина 
совпадает с главным удлинением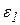 
. Можно записать:
|
|
|
.
Интенсивность деформации сдвига:
.
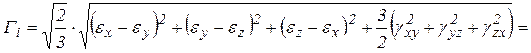
Последние обобщенные характеристики деформированного состояния точки, как и тензор деформаций, полностью характеризует деформированное состояние, т. к. под радикалом присутствуют все компоненты тензора деформаций.
17. Обобщенные характеристики деформированного состояния точки.
См. 16
18. Неразрывность деформаций, уравнения неразрывности деформаций.
Перемещение любой точки сплошного тела определяется тремя функциями 
, деформации точки определяются шестью функциями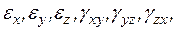 
По известным перемещениям можно определить все шесть составляющих деформаций. Все шесть деформаций нельзя задать произвольно, между ними должны существовать определенные зависимости. Число таких зависимостей равно шести, и они делятся на две группы. Первая группа – зависимости между составляющими деформаций в одной плоскости, вторая группа – зависимости между составляющими деформаций в разных плоскостях.
Первая группа
Из геометрических уравнений продифференцируем два первых уравнения:
, 
.
Складывая почленно эти уравнения, получим
.
Или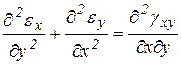 
.
Вторая группа
Дифференцируя уравнения для определения одинаковых деформаций по координатам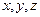 
и складывая два и вычитая третье, получим после преобразований и дифференцирования по 
.
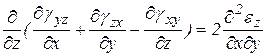В итоге имеем систему уравнений
,
,
,
,
,
.
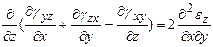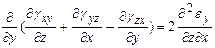Уравнения получены Сен-Венаном, называются уравнениями (условиями) совместимости или неразрывности деформаций. Условия совместимости линейных деформаций для осесимметричной задачи 
.
Физический смысл этих уравнений таков, заданное тело, сплошное и непрерывное до деформации, остается сплошным и непрерывным, и после деформации. Если по заданным нагрузкам определить напряжения и деформации, то при этом необходимо одновременно удовлетворить и уравнение неразрывности. В противном случае возникают противоречия. Энергетический смысл уравнений неразрывности заключается в том, что осуществление этого принципа соответствует минимальной потенциальной энергии, накапливаемой телом.
|
|
|
|
|
|
