 |
24. Общая характеристика теорий пластичности.
|
|
|
|
24. Общая характеристика теорий пластичности.
На базе обобщенного закона Гука в теории пластичности широкое распространение получили две теории: теория малых упругопластических деформаций и теория приращения пластических деформаций или теория пластического течения.
2. 1. 1. Деформационная теория пластичности
Выше было показано, что существует подобие диаграмм Мора для напряжений и деформаций в упругой области. Это положение является справедливым и для пластической области в условиях простого нагружения. Кроме этого направления главных линейных деформаций (удлинений) должно совпадать с направлением главных нормальных напряжений. В соответствии с положением о подобии диаграмм Мора в каждый момент пластической деформации имеет место соотношение:
,
где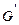 
– модуль пластичности второго рода, являющийся величиной переменной
Из соотношений 
, 
, и условия несжимаемости 
, определим значение 
:
.
Поступая аналогичным образом с другими сочетаниями уравнений, получим с учетом 
:
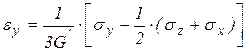
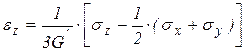
Коэффициент 
перед суммами напряжений представляет собой коэффициент Пуассона. Из последних выражений следует, что выражения для пластических деформаций аналогичны выражениям для упругих деформаций с той лишь разницей, что модуль упругости первого рода заменен модулем пластичности первого рода, при этом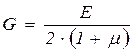 
, а при 
, 
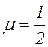, где 
- модуль пластичности первого рода, величина переменная.
Из обобщённого закона упругости можно сделать ряд выводов, которые используются в теории пластичности. Например, линейное напряженное состояние и объёмное определяются уравнениями связи формально одинакового вида 
, 
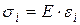, тогда 
.
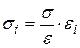Полученное соотношение, в какой-то степени, объясняет гипотезу единой кривой. При пластической деформации в случае сложного напряженного состояния могут появиться области, где направление процесса (нагружение или разгрузка) может изменяться. Нагружение сменяется разгрузкой и наоборот. Это приведет к изменению главных направлений девиаторов деформаций и напряжений. Поэтому при сложном напряженном состоянии нагружение может быть как простым, так и сложным.
|
|
|
Связь напряжений и деформаций при простом нагружении в зоне пластического течения с учетом условия постоянства объема, т. е. :
,
тогда:
; 
,
; 
,
; 
.
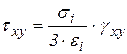Применение деформационной теории пластичности может быть использовано в случае простого или близкого к нему нагружения. Выражением простого нагружения в процессах обработки металлов давлением является понятие монотонности. Условие монотонности позволяет распространять деформационною теорию пластичности, созданную для малых упругопластических деформаций, на конечные, т. е. большие деформации, которые сопровождают процессы ОМД.
25. Условие постоянства объема при пластической деформации.
При пластической деформации объем упруго не деформируется. Соблюдается закон постоянств объема. Запишем условие постоянства объема при пластической деформации в виде 
, где 
- текущие значения высоты, ширины и длины полосы. Продифференцируем это выражение:
,
или
,
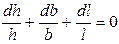где 
- элементарное относительное обжатие по высоте, 
- элементарное относительное уширение полосы,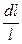 
- элементарное относительное удлинение полосы. В расчетах пользуются показателями деформации:
, 
, 
.
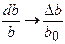Введем обозначения 
, 
, 
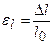, где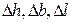 
- абсолютные изменения размеров по высоте, ширине и длине. При малых деформациях менее 5% условие постоянства объема:
.
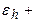
В теории упругости и пластичности часто пользуются значениями линейных деформаций 
. Для малых деформаций можно записать условие постоянства объема в виде:
|
|
|
.
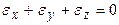При больших деформациях такие записи дают ошибочный результат, тем больший, чем больший процент пластической деформации. Большие пластические деформации:
- истинное относительное обжатие;
- истинное относительное уширение;
- истинное относительное удлинение.
В этом случае имеет место точное выполнение условия постоянства объема:
.
В теории пластического течения условие постоянства объема запишется:
.
С точки зрения приемлемости результата в теории пластичности широко используется теория пластического течения или теория приращения деформаций, где применяются скорости деформаций по различным направлениям.
|
|
|
