 |
1.3.2. Связь напряжений и деформаций для пространственного
|
|
|
|
1. 3. 2. Связь напряжений и деформаций для пространственного
напряженного состояния
Часто возникает необходимость выразить напряжения через деформации. Решим уравнения обобщенного закона Гука относительно  :
:
 ,
,
 ,
,
 .
.
Пусть:
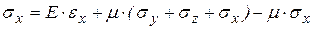 ,
,
 .
.
Определим  . Суммируя напряжения, получим:
. Суммируя напряжения, получим:
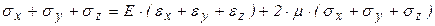 ,
,
или
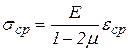 ,
,
где -  ,
,  .
.
Тогда:
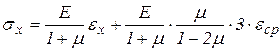 .
.
Или
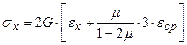 ,
,  ;
;
 ,
,  ;
;
 ,
, 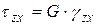 .
.
Выражения также определяют запись обобщенного закона Гука для объемного напряженного состояния через деформации. Для нормальных напряжений можно записать:
 ;
;  ;
;  ,
,
где 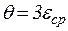 (объемная деформация),
(объемная деформация), 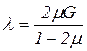 (постоянная Ляме).
(постоянная Ляме).
Определяя разность, имеем:
 ;
;  ;
;
 .
.
Из последних соотношений определяется подобие кругов Мора для напряжений (  ) и для деформаций (
) и для деформаций ( 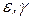 ). Применительно к «главному кубу», можно показать, что:
). Применительно к «главному кубу», можно показать, что:
 ;
;  ;
;  .
.
Получим упрощенную запись обобщенного закона Гука, используя выражение для обобщенного напряжения, действительно:
 =
=
 =
=

Учитывая, что:

Имеем:
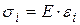 .
.
Интенсивность напряжений прямо пропорциональна интенсивности деформаций. Если в процессе простого и сложного нагружения для каждого последующего момента времени интенсивность напряжения  и интенсивность деформации
и интенсивность деформации 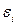 превышают их значения для предыдущего момента времени, то такой процесс деформации называется активным. В противном случае – пассивным. Это имеет значение для теории пластичности, где имеет место различие законов нагрузки и законов разгрузки.
превышают их значения для предыдущего момента времени, то такой процесс деформации называется активным. В противном случае – пассивным. Это имеет значение для теории пластичности, где имеет место различие законов нагрузки и законов разгрузки.
1. 3. 3. Закон упругого изменения объема и закон упругого изменения формы
Ранее было получено выражение:
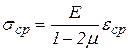 .
.
Среднее напряжение прямо пропорционально средней деформации. Так как,  , то
, то  . Среднее напряжение в точке пропорционально объёмной деформации в окрестности той же точки.
. Среднее напряжение в точке пропорционально объёмной деформации в окрестности той же точки.
|
|
|
Выражения определяют закон упругого изменения объёма. Этот закон справедлив и при высоких значениях гидростатического давления, значительно превышающих обычный предел упругости материала.
Если в выражениях для нормальных напряжений отнять от левых и правых частей величину  , тогда:
, тогда:
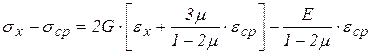 .
.
Подставляя  , получим
, получим  .
.
В итоге:
 ;
;  ,
,
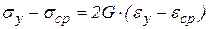 ;
;  ,
,
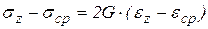 ;
;  .
.
Выражения широко применяются в теории пластичности. Если левые и правые части выражения назвать компонентами напряжений изменения формы с компонентами деформаций изменения формы, то обобщенный закон упругости является законом изменения формы. Формулируется так: компоненты напряжений и деформаций, соответствующие изменению формы, пропорциональны друг другу.
Систему зависимостей можно представить в виде таблицы
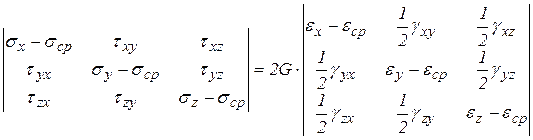
Как известно, левую матрицу называют девиатором напряжений, а правую – девиатором деформаций, тогда
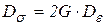 .
.
Девиатор напряжений пропорционален девиатору деформаций. Выражения определяют также закон изменения формы.
Используя закон изменения объема и понятие о шаровых тензорах, имеем:
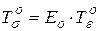
т. е. шаровой тензор напряжений пропорционален шаровому тензору деформации, где
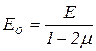 .
.
21. Связь деформаций и напряжений.
Известна связь между напряжением и деформацией при одноосном напряженном состоянии, установленным Гуком:
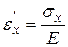 ,
,
где 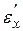 - относительные удлинения параллелепипеда вдоль оси
- относительные удлинения параллелепипеда вдоль оси 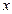 под действием одного напряжения
под действием одного напряжения  ,
,  – модуль упругости материала.
– модуль упругости материала.
В направлении осей 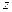 и
и  , поперечных к действующей силе, имеет место деформация согласно закону Пуассона:
, поперечных к действующей силе, имеет место деформация согласно закону Пуассона:
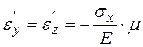 ,
,
где 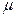 - коэффициент Пуассона.
- коэффициент Пуассона.
Соответственно для напряжений 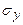 и
и 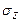 имеем:
имеем:
 ,
, 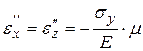 ,
,
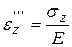 ,
,  .
.
Так как между напряжениями и деформациями линейная зависимость, то действует принцип суперпозиции или закон независимости действия сил, согласно которому:
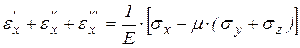 ;
; 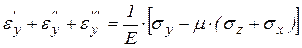 ;
;
 .
.
Выражения предполагают, что не существует перекашивания прямых углов на гранях (углы сдвига) элементарного параллелепипеда.
|
|
|
Действие касательных напряжений искажают форму параллелепипеда. Принимается, что касательные напряжения или деформации сдвига не зависят от нормальных напряжений или линейных удлинений. Совокупность касательных напряжений 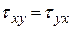 , вызывает перекашивание граней, параллельных плоскости
, вызывает перекашивание граней, параллельных плоскости  и оставляют без изменения другие грани. В соответствии со вторым законом Гука:
и оставляют без изменения другие грани. В соответствии со вторым законом Гука:
 ;
;  ,
,
где 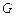 – модуль упругости второго рода. Известно, что
– модуль упругости второго рода. Известно, что 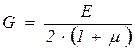 .
.
От действия напряжений 
 ;
; 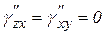 ,
,
от касательных напряжений 
 ;
; 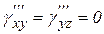 .
.
Все компоненты напряжений определяют составляющие деформаций:
 ,
,  ;
;
 ,
, 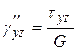 ;
;
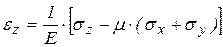 ,
,  .
.
Последние выражения представляют собой обобщенный закон упругости для изотропного тела.
Компоненты тензора деформаций в данной точке тела находятся в линейной зависимости от компонентов тензора напряжений в той же точке.
При 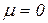 компонент тензора напряжений прямо пропорционален соответствующему компоненту тензора деформации.
компонент тензора напряжений прямо пропорционален соответствующему компоненту тензора деформации.
|
|
|


